一、刚体平面运动的运动方程
1、刚体平面运动简化
刚体平行于某固定平面

平面运动刚体上
因此,在刚体的平面运动分析中,可以只选取刚体上的一个平行于固定平面的平面来分析即可。于是将三维物体变为二维平面进行研究,实现了降维,简化刚体的平面运动。
2、刚体平面运动方程
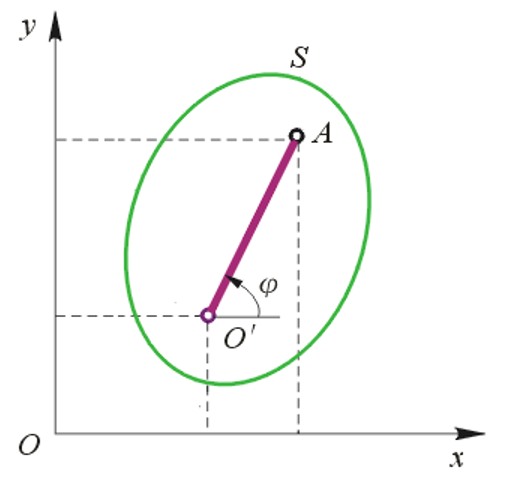
确定直线
3个独立变量随时间变化的函数,即为刚体平面运动方程:
点
二、平面图形运动的分解
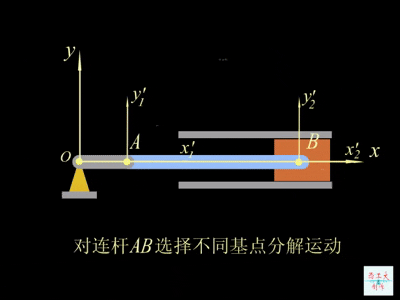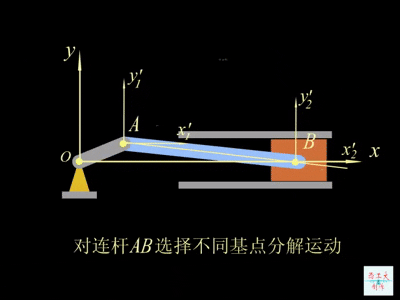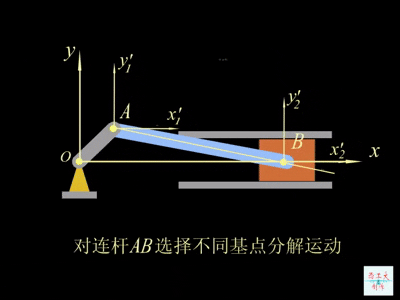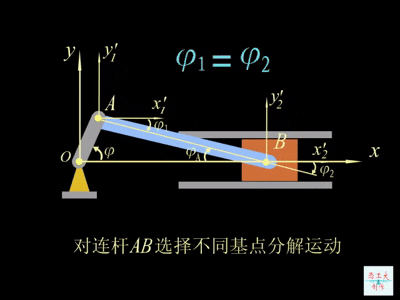
刚体的平面运动可以分解为随同基点的平移和相对基点的转动。可以任意选择基点,在基点上建立平移系(特殊的动系),在刚体平面运动的过程中,平移系只发生平移。刚体平面运动(绝对运动)可以分解为跟随平移系的平移(牵连运动),以及平面图形相对于平移系的转动(相对运动)。
平移的轨迹、速度与加速度都与基点的位置有关,但是转动角速度与基点的位置无关。因为平移系(动系)相对定参考系没有方位的变化,平面图形的角速度既是平面图形相对于平移系的相对角速度,也是平面图形相对于定参考系的绝对角速度。如动图所示:
三、平面图形上各点的速度
1、基点法
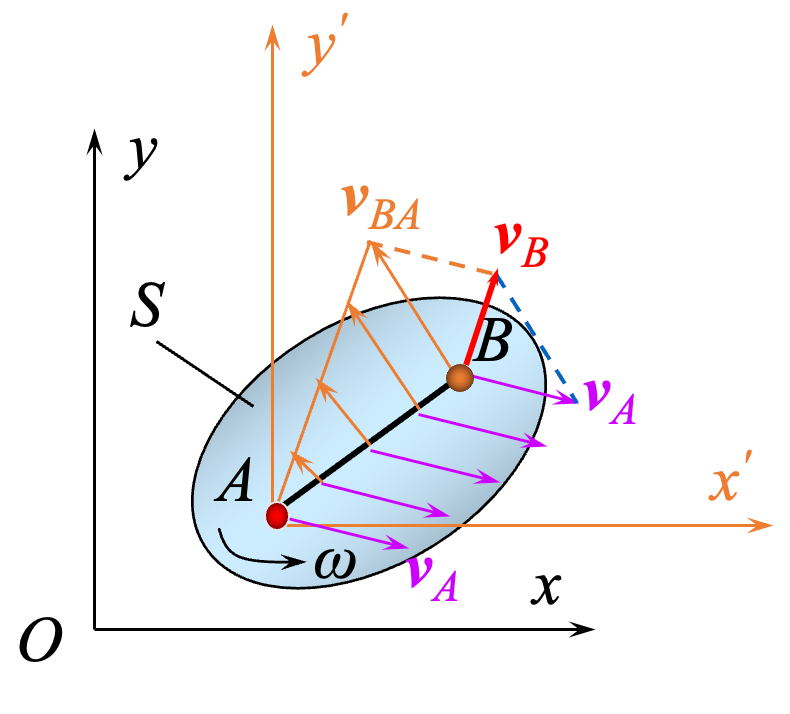
选取基点为
得到:
平面图形内任意点的速度,等于基点的速度与该点绕基点相对转动速度的矢量和。
2、速度投影法
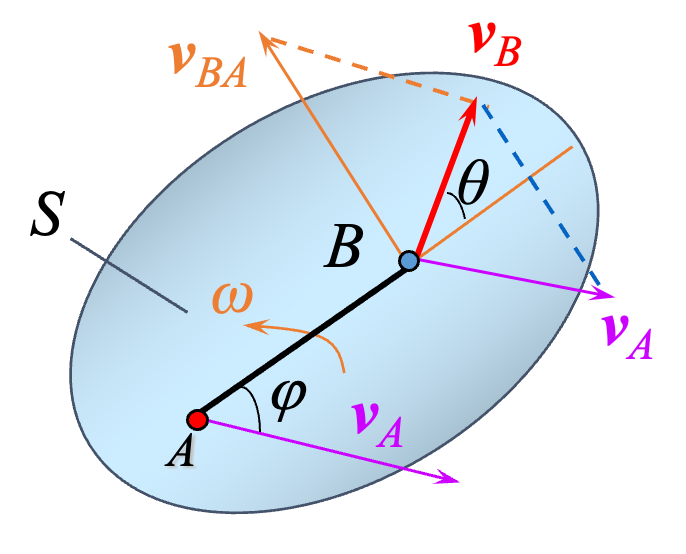
根据速度合成定理:
上式等号两侧分别向
可以写作:
这种方法的原理就在于刚体的特性,刚体不会发生形变,以至于
3、速度瞬心法
(1) 瞬心
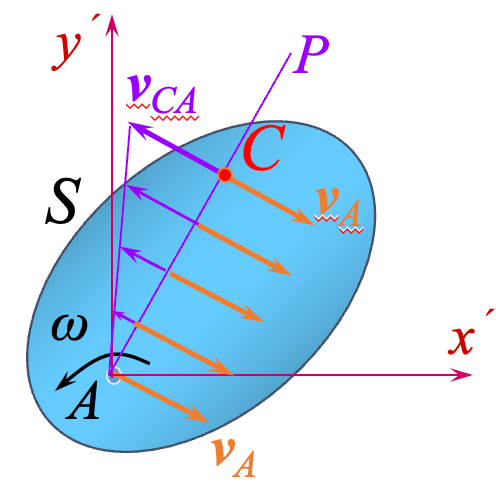
平面图形
- 跟随基点平移的速度
,这是牵连速度,各点速度相同。 - 相对于平移系的速度
,这是相对速度,自 点起线性分布。
在直线
(2) 速度瞬心法
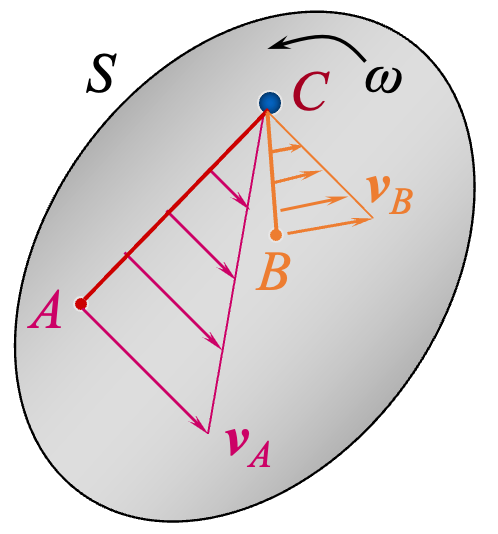
当平面图形在
这种运动不能看成是刚体的定轴转动,因为定轴转动的轴是固定的,而瞬心会随着刚体的运动而变化。
根据速度合成定理,平面图形上任一点,如
其中:
图形内各点的速度的大小与该点到速度瞬心的距离成正比,其方向垂直于该点与速度瞬心的连线,指向转动前进的一方。应用瞬时速度中心以及平面图形在某一瞬时绕速度瞬心作瞬时转动的概念,确定平面图形上各点在这一瞬时速度的方法,称为速度瞬心法。
(3) 速度瞬心位置确定
-
第一种情形:
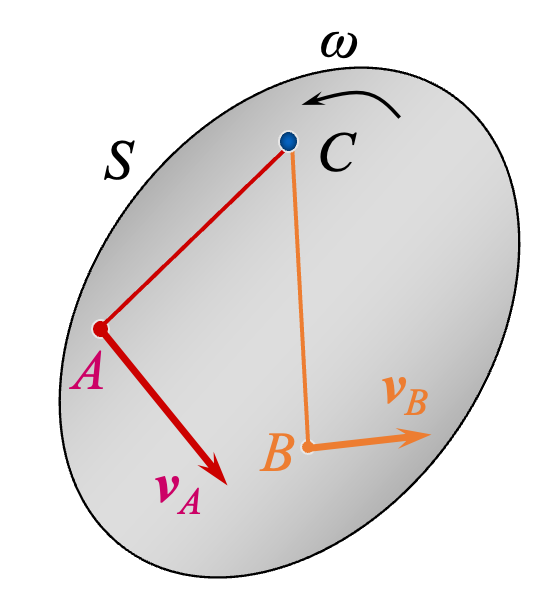
已知平面图形上两点的速度矢量的方向,这两点的速度矢量方向互不平行。
-
第二种情形:

已知平面图形上两点的速度矢量的大小与方向,而且两矢量互相平行,并且都垂直于两点的连线。
-
第二种情形推论:
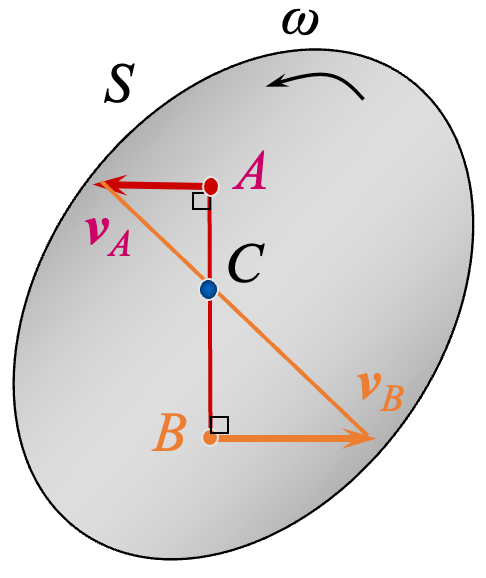
已知平面图形上两点的速度矢量的大小与方向,而且两矢量互相平行、方向相反,但二者都垂直于两点的连线。
-
第二种情形的特殊情形:
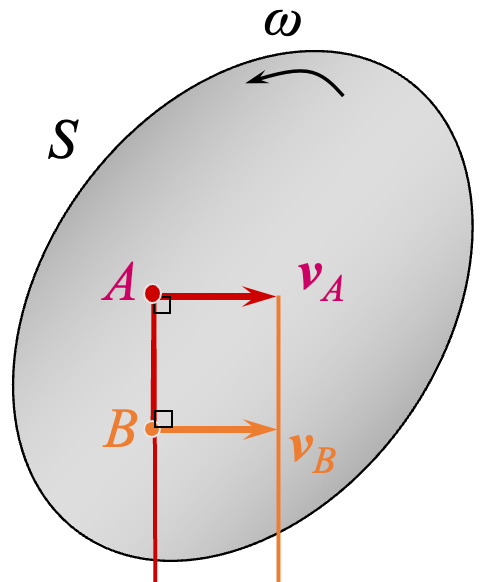
,大小相同,指向相同,这种情况下瞬心在无穷远处,表示刚体在做瞬时平移运动,角速度为 。刚体做瞬时平移运动,表示刚体各点的速度相同,但是不代表各点的加速度相同。 -
第三种情形:
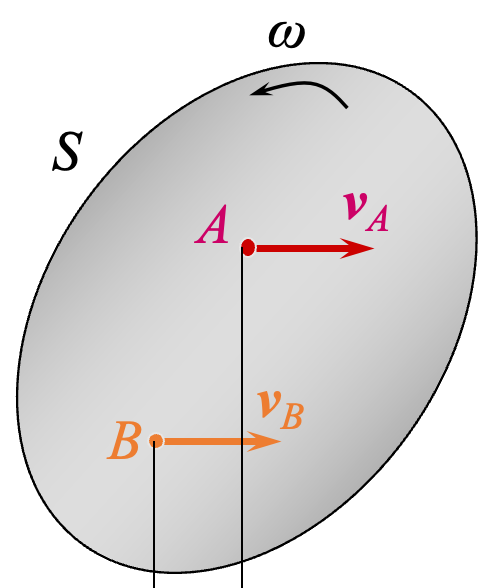
已知平面图形上两点的速度矢量的大小与方向,而且两矢量互相平行、方向相同,但二者都不垂直于两点的连线。在这种情况下,瞬心也是在无穷远处,表示刚体在做瞬时平移运动,角速度为
。 -
第四种情形:

车轮沿固定面只滚动而不滑动时,车轮与固定面的接触点
的速度为零。点 就是车轮的速度瞬心。
(4) 速度瞬心的特点
-
瞬时性:不同的瞬时,有不同的速度瞬心;因此瞬心具有加速度。瞬心的轨迹有两种:动瞬心轨迹——在
上看瞬心的轨迹;定瞬心轨迹——瞬心绝对运动轨迹。动瞬心轨迹沿定瞬心轨迹作无滑动的滚动。 
-
唯一性:某一瞬时只有一个速度瞬心。
-
瞬时转动特性:平面图形在某一瞬时的运动都可以视为绕这一瞬时的速度瞬心作瞬时转动。
四、平面图形上各点的加速度
1、基点法
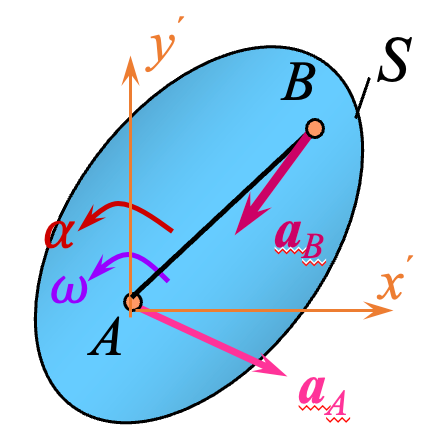
如果已知平面图形上一点
平面图形上任意一点的加速度等于基点的加速度与这一点对于以基点为坐标原点的平移系的相对切向加速度和法向加速度的矢量和。
2、加速度瞬心法
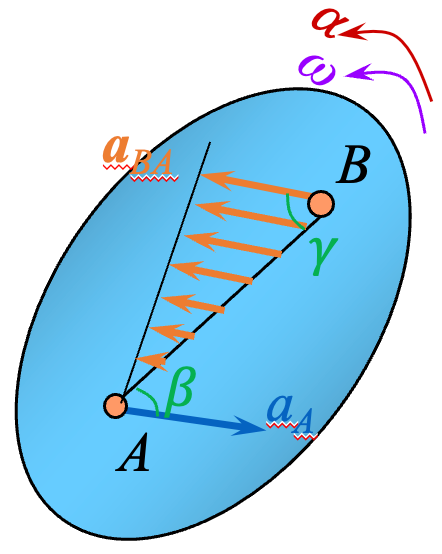
取
3、加速度投影法
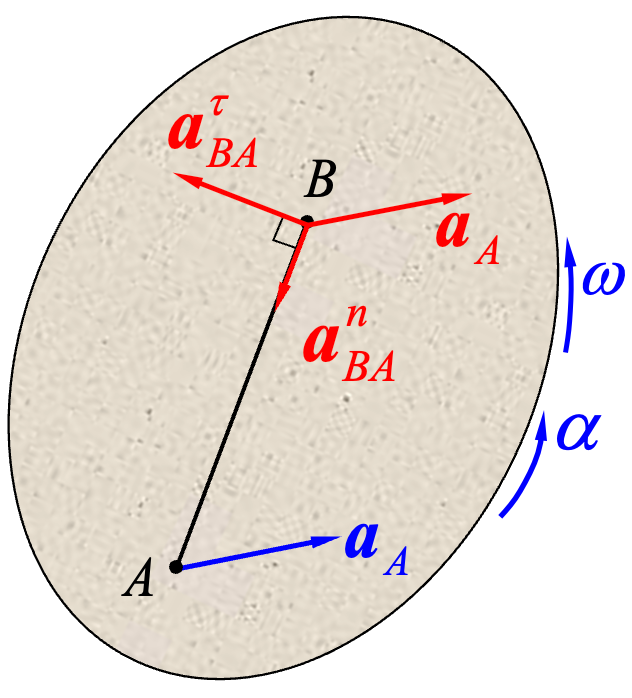
如图:
当
当
使用的限制条件过多,所以很少使用加速度投影法。
