一、留数定理
1、留数
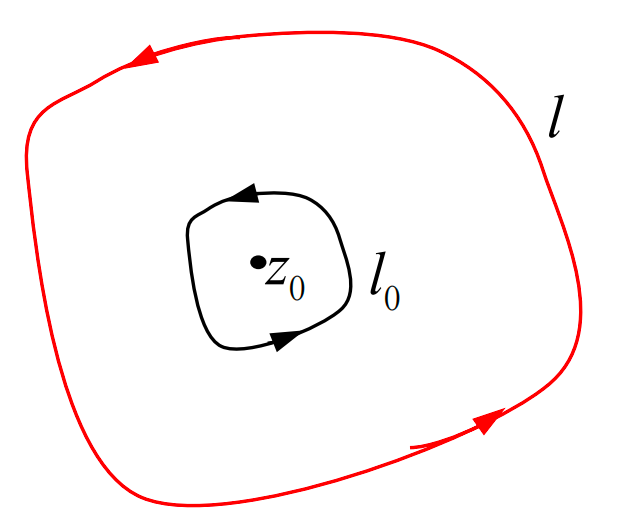
如果复变函数
在洛朗级数的收敛环中取任意一个包围
根据这个例子,可得:
所以可以得到结论,对于任意包围了
从在复变函数的积分来看,洛朗级数展开中系数
函数
2、柯西留数定理

设函数
也就是说:
证明:在每个奇点附近作只包含该奇点的小回路:
。每个小回路只包含一个奇点,所以: 函数在小回路外的多连通区域中解析,按照多连通区域的柯西积分定理:
3、无穷远处的留数
无穷远处的留数:如果无穷远处
在回路正向(奇点为无穷远,积分区域在外,这里是顺时针方向)的积分为:
定义无穷远处的留数:
所以有(积分区域在内,方向为逆时针方向):
这与有限元点的留数定理结果一致。使用代换
于是可以得出一个定理:函数
4、留数计算
(1) 一阶极点处的留数
如果
因此:
也就是说:
对于有理函数:
更一般:
(2)
如果
如果
从而可以得到:
(3) 函数直接展开法
对于高阶极点的留数,有时候利用函数直接展开法更为有效
那么
5、极点次数判断定理
极点次数的判断定理:
如果
二、应用留数定理计算实变函数定积分
1、类型一:
作变换
回代到原积分中:
根据留数定理:
也就是将
2、类型二:
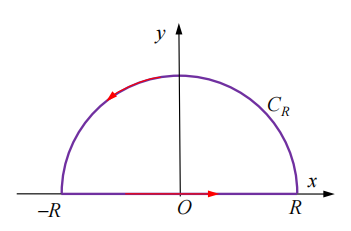
为了应用柯西留数定理来求得等式右边的积分,我们人为地在复平面上构造一个如图所示的围道(封闭的路径),包括一个半圆
在实轴上
当半径
下面我们讨论在何时满足
-
函数
是有理函数, ( 指多项式的最高幂次),上式成立。 -
当半径
时, (一致趋向于零),上式也成立。
证明:利用不等式:
是多项式当 足够大时: 当半径
时, (一致趋于零),上式也成立。
更一般地,可以推导大圆弧定理:
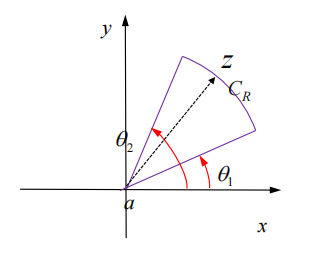
证明:
记
一致趋向于 , ,当 : 由于
的任意性: 大圆弧定理得证:
3、类型三
对于这类积分,指数函数可以利用欧拉公式分解为两部分:
所以我们可以通过计算类型三所示积分的值,取其实部或者虚部来获得上述两种实变函数的定积分。
首先我们需要使用 Jordan(约当)引理:
该引理的证明不做要求。

和第二类问题类似,我们需要构造一个围道,该围道由实轴和一个半圆所组成(至于半圆位于上半平面还是下半平面,需要根据
分别比较等式两边实部和虚部的值,就可以得到:
当积分表达式中的
4、特殊情况:实轴上有单极点(一阶极点)的情形
如果
定义瑕积分的主值为:
对于上面的反常积分,我们考虑分的主值为:
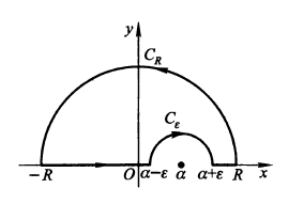
当实轴上存在瑕点的时候,为了绕开瑕点处函数的奇异性,需要以瑕点为圆心,作一个足够小的圆,构造如图所示的围道。柯西留数定理对于该围道所围成的区域依旧成立。
对于函数沿外面半圆
对于瑕点附近的内部半圆,需要用到小圆弧定理:
这里
证明:
记
一致趋向于 , ,当 : 由于
的任意性:
