一、电偶极子

考虑两个等量异号的点电荷 和 ，分别位于 和 ，即沿 轴对称分布。定义电偶极矩为

方向为负电荷指向正电荷，大小为电荷与距离的乘积

1、电偶极子在上产生的电场

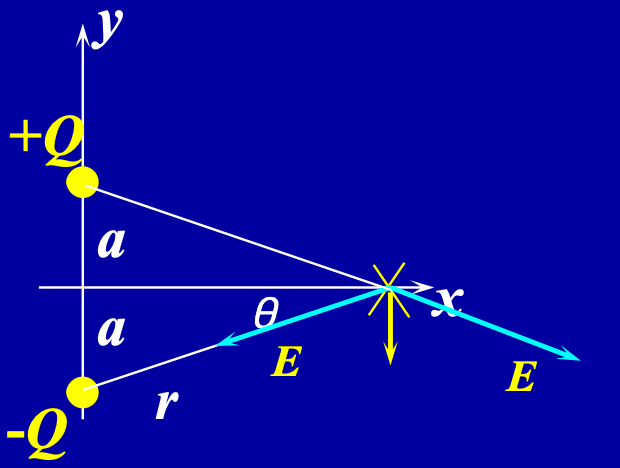
由对称性，，只需要计算：

其中：

所以：

2、电偶极子在上产生的电场

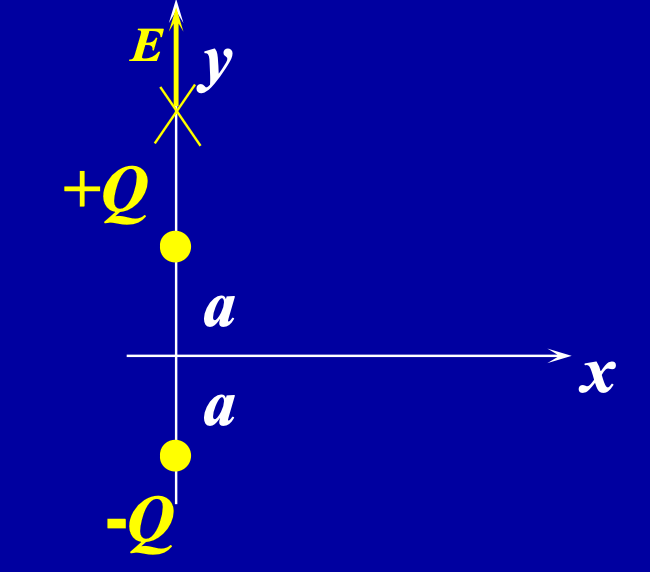
在轴上，，只需要计算：

化简得：

3、电偶极子在电场中的受力分析

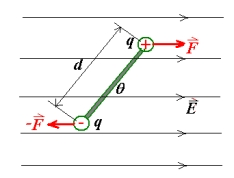
上图为电偶极子在均匀电场中的受力分析。很明显，电偶极子收到一个力矩作用，首先写出电偶极矩矢量：

分析受力特点，整体受力为，合力矩为：

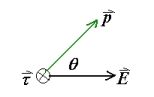
即：

以电偶极子的中点为参考点，计算电场对电偶极子做的功：

二、连续电荷分布产生的电场

1、无限长带电直线在某一点产生的的电场

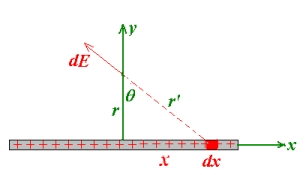
根据上图演示，计算在该点产生的电场：

其中和为:

代入得：

其中与并不是独立的，存在下面关系：

所以：

将向两个方向分解：

积分得：

经过上面的推导，得出结论：无限长带电直线对某一点产生的电场，随着该点到直线的距离成反比例减小。

2、均匀带电圆环在圆心轴上某点产生的电场

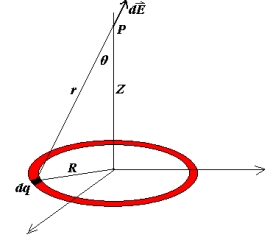
计算对该点产生的电场：

由对称性得：

计算在竖直方向的分量：

积分得：

在两种特殊的情况下：

3、均匀带电圆盘在圆心轴上某点产生的电场

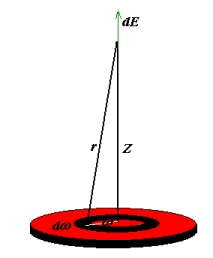
计算单位面积上带有的电荷：

将均匀带电圆盘看作是无数个圆环叠加：

积分得：

当圆盘无限大时：

当点离圆盘足够远时，可以将圆盘近似看成点电荷：