一、通量

通量的计算公式：

其中为速度，为面积矢量，方向为其任意法向。

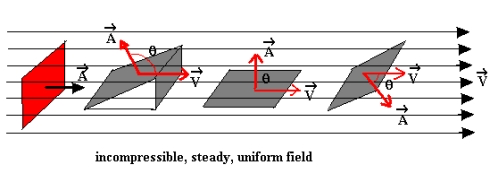
二、高斯定理

1、闭合曲面的通量

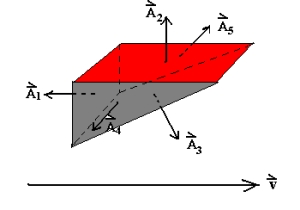
任意形状的闭合曲面，规定面积的法向指向外，流入该曲面的通量与流出该曲面的通量相等，也就是说，闭合曲面的流量代数和为。

所以，如果闭合曲面内没有源，则：

如果闭合曲面内有源，则：

如果闭合曲面内有汇，则：

2、电通量

电通量可以理解为通过单位面积通过的电力线的数目，根据闭合曲面的通量公式，写出电场的通量公式：

其中的方向指向闭合曲面外。

若闭合曲面内没有电荷，则上式值为，即：

3、电场高斯定理

从任意封闭曲面内流出的电场的通量与封闭曲面包围的电荷成正比，与电荷的分布无关，其值为：

其中为闭合曲面包围的电荷量，为真空介电常数。该公式永远成立。

三、高斯定理的应用

1、在球面上应用高斯定理

如果在空间中的每一点的电场方向与面积法向完全相同，则有：

如果球面上的每一点电场大小相同（即电荷集中在球心），恒为，则可以将提出到积分之外：

那么在这个球上使用高斯定理，得到：

即：

这与库仑定律的结论完全相同。

2、在均匀带电球体上应用高斯定理

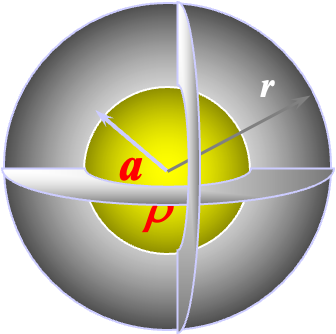
假设实心球体的半径为，电荷体密度为。我们分三种情况讨论这个问题

(1) 研究点在球体内（）

研究点离球心的距离为，我们研究一个半径为的高斯面，根据高斯定理：

得到：

这与点电荷产生的电场表现相同。

(2) 研究点在球面上（）

研究方法相同，但是根据万有引力部分的推导，在所选取的高斯面外的带电部分所产生的电场相互抵消，则有：

得到：

3、在导体上使用高斯定理推导导体带电情况

我们已知导体内部电场为，通过高斯定理，选取略小于导体表面的闭合曲面做高斯面，则根据高斯定理可知，导体内部的电荷。即导体所带电荷全部分布在导体的表面。

4、在均匀带电的无限长直线上应用高斯定理

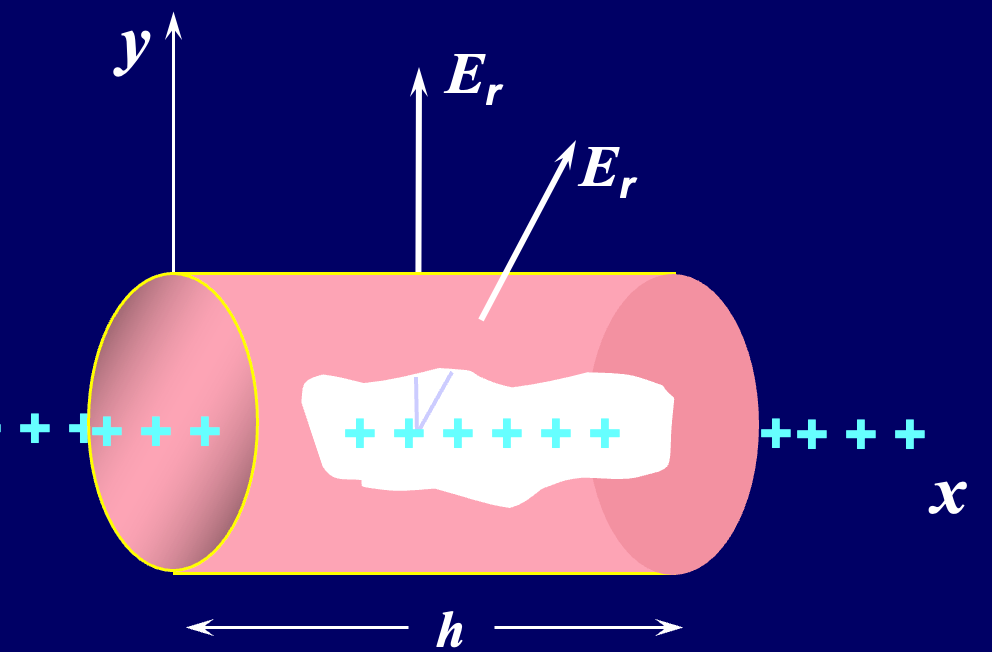
利用对称性可知，由于导体是无限长的，则在方向上无电场，电场方向全部垂直于直线，且大小只与该点离直线的距离有关。所以我们选取一个高度为，半径为的圆柱作为高斯面来研究电场中某一点的电场。使用高斯定理：

直线的线密度为，则高斯面内包裹住的电荷为：

得到：

5、在均匀带电的无限大平面上应用高斯定理

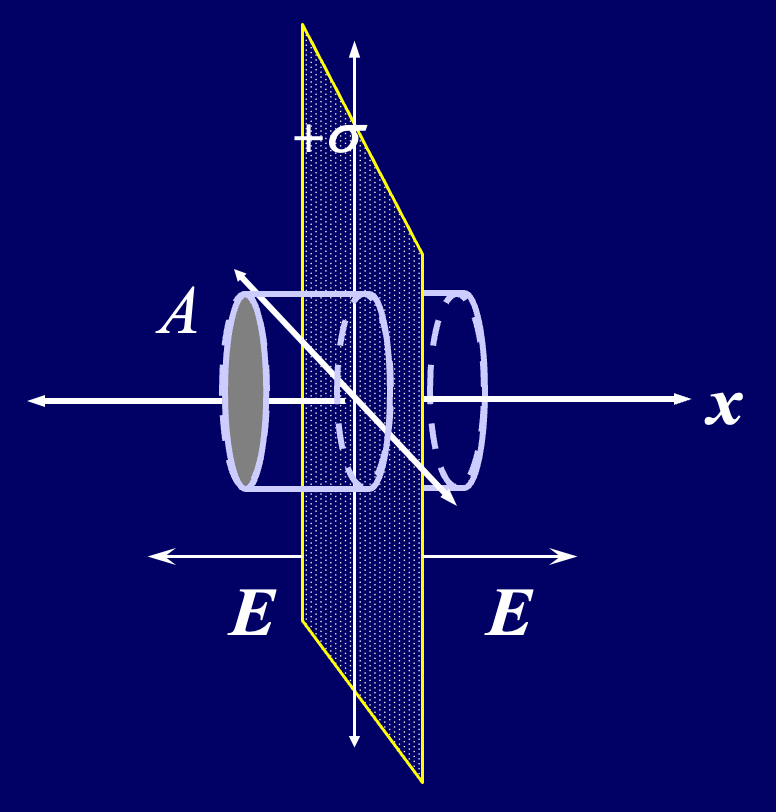
利用对称性可知，由于导体是无限大的，则只有方向上的电场，我们选取一个圆柱面作为高斯面截取平面的一部分，圆柱的顶面面积为。使用高斯定理：

代入电荷的面密度，得到：

6、无限大平行板电容器

无限大平行板电容器可以看作是两个无限大均匀带电平面，且电性相反。使用相同的取高斯面方法同时分析两个平面或者直接两个场叠加，可知两平行板外侧电场为，内部为。