一、函数级数与复（函）数级数

1、函数级数相关性质

(1) 函数级数

如果级数每一项都为函数：

则称其为函数级数。

(2)函数级数的点收敛性（单点收敛）

如果对于某一个点，级数收敛，那么我们称级数在收敛。

(3)函数级数的区域收敛性（逐点收敛）

如果级数对于区域内的每一点都收敛，那么我们称级数在区域收敛。

(4)级数的一致收敛性（一致收敛）

对于，与无关的，当正整数 时，和成立：

如果在区域内，，与无关，收敛，则在区域内绝对且一致收敛。

2、一致收敛的性质

1. 一致收敛的级数， 如果每项连续，那么其和函数也连续；求极限（连续性）可以与求和交换次序，求积分与求和可以交换次序。

2. 魏尔施特拉斯定理：一致收敛的级数，如果每项解析，那么和函数也是解析。导数与求和可以交换次序，也就是说，可以先逐项求导，然后再求和。求导后再求和得到的级数在区域内也是一致收敛。

3、复数级数

对于复数级数或者复函数级数，可以分解两个级数：一个级数与实部相关， 另一个级数与虚部相关，所以可以归结为两个实数级数的收敛性问题。

二、幂函数

1、收敛圆与收敛半径

下面我们将讨论以为中心的幂级数(每项都是幂函数)问题：

考察由各项的模所组成的正实数级数的收敛性：

如果幂级数在圆内绝对收敛，在圆外 发散，那我们称这个圆为收敛圆，圆的半径为收敛半径。 说明除外处处发散， 说明处处都是收敛。

可以使用达朗贝尔比值判别法和柯西根值判别法等证明收敛性。

2、阿贝尔第一定理

如果幂级数在某点收敛，则在以为圆心，为半径的圆内 绝对收敛，在闭圆内一致收敛。

证明：已知：

存在，使得：

对于任意，有：

当时，级数：

收敛（这是一个等比级数），所以：

在 内绝对收敛。

再考虑一致收敛性。令 ，则

由于

收敛（ 判别法），所以

在 内一致收敛。

3、幂级数的解析性

连续函数的幂级数展开为：

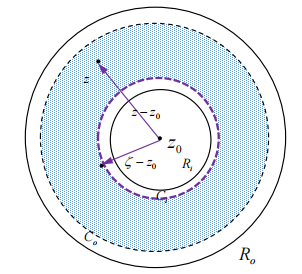
如上图所示，考虑半径略小于收敛半径的圆：

对于圆内的任意一点及圆上的任意点

两边沿圆周进行路径积分：

根据柯西积分公式可以得到：

也就是说，幂级数可以表示为一个连续函数的回路积分。根据柯西型积分的解析性定理，可以得到：幂级数在其收敛圆内部是一个解析函数，在收敛圆内不会出现奇点。

三、泰勒级数展开

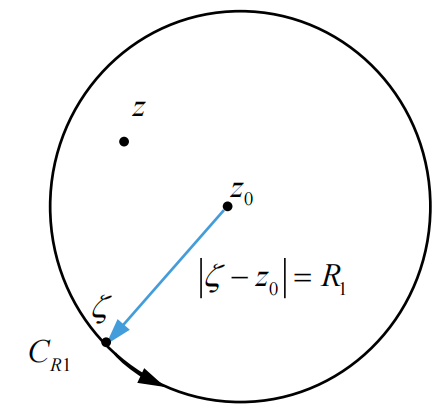
设在以为圆心的圆内解析，则对圆内的任意点，可展为幂级数：

上式成为函数以为中心的泰勒级数。

证明：应用柯西公式：

对积分函数分母进行配凑：

得到：

因为，得到：

回代到中：

由于级数是一致收敛的，积分和求和可以交换顺序，并使用高阶柯西公式，得到：

多值函数在规定好单值分支后，在其解析区域内也可以做泰勒展开。

四、解析延拓

1、解析延拓的解释

当我们在一定区域内确定了一个解析函数之后，考虑能否把它延拓到更大范围 上的解析函数，要求延拓后函数在上和解析函数相同，这就是解析延拓。简单地说，解析延拓就是解析函数定义域的扩大。

通常可以用泰勒级数进行解析延拓：在解析函数延拓前的区域中任选一点，求得解析函数在该点的各阶导数，然后在该点附近对原来的解析函数进行泰勒展开，分析泰勒级数展开的收敛半径，如果该收敛半径超过了延拓前函数的定义域范围，表明延拓成功。

2、解析函数的零点

函数的零点：函数在解析，那么可以在该点附近进行泰勒展开

如果称为函数的m阶零点。

函数在解析，而且。

3、零点的孤立性定理

设函数在区域内解析，若在内的一个子集中恒等于零，那么在区域G内恒等于零。设在区域内解析且不恒等于零，为其零点。则必能找到的邻域，使在此邻域内是的唯一零点。

4、解析延拓的唯一性定理

设在区域内解析.若在内存在的无穷多个零点，且无穷多个零点有极限：,那么f(z)内恒为零。

证明： 根据函数的连续性：，所以也是函数的零点。如果函数不恒为零，由零点的孤立性定理，存在的某个邻域，在此邻域内是其唯一的零点，这与上面的条件矛盾，所以，函数只能恒为零。

于是可以得出解析延拓的唯一性定理：设在区域内有两个解析函数和, 在内存在无穷多个点，，而且。那么在该区域内，。

五、洛朗级数展开

当所研究的区域上存在函数的奇点（也就是函数不解析）时，无法展开成泰勒级数，需要考虑在去除奇点后的环域上进行展开。

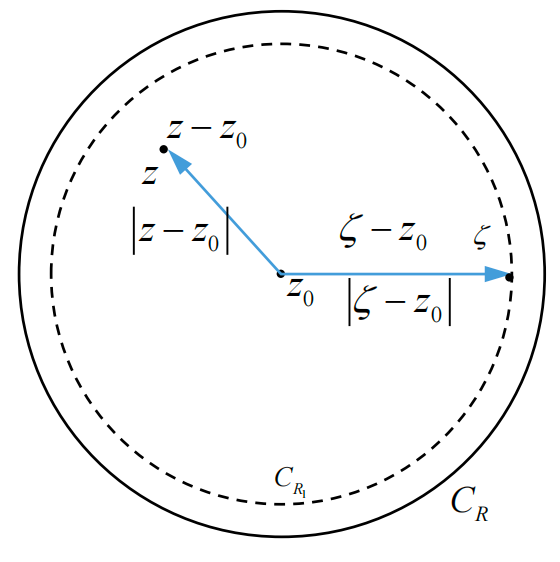
对于下面的双边幂级数（同时存在正幂次项和负幂次项）：

只有两部分级数都收敛才能保证原来级数的收敛性，对于正幂次部分，可以使用之前学过的级数判别法来求出其收敛半径，收敛范围为：。对于负幂次项部分，引入新的变量：：

于是可以分析其收敛半径，回代得到原级数的收敛半径（圆的外部收敛），得到其收敛范围为：。

• 如果，则双边区域在环内绝对且一致收敛，其和为一解析函数，级数可逐项求导。该环域称为该双边幂级数的收敛环。
• 如果，则该级数处处发散。

于是，我们可以得出洛朗级数定理，其中：

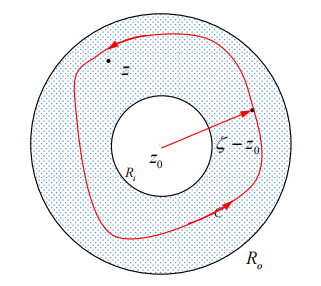
设 在环形区域 的内部单值解析，那么对于环形区域内任一点， 都可展开为如下的幂级数:

其中 是环形区域内任意一条简单的封闭曲线，积分方向为常规逆时针。由于函数不在封闭曲线的区域内解析，与泰勒展开不同，这个系数和导数之间没有关系。所以计算相当复杂，一般会采取其他方法获取其级数形式。

证明：

证明：将外圆稍稍缩小为，内圆稍稍扩大为 ，对于任意位于和所围成的区域中点，应用多连通区域柯西积分公式：

沿外圆 ： ，有：

沿内圆 ，有：

综合起来：

对于后面这一项，令，则：，有：

所以，刚才的积分表达式为：

在环形区域上，积分项中的，所以上述积分项中每一项在和所围成的区域中是解析的。根据柯西定理，对于该区域内任意一条简单的封闭曲线，始终成立。

所以可以得到如下的洛朗级数表达式：

证毕。