一、力对点的矩和力对轴的矩

1、力对点的矩

(1) 力对点之矩的定义

力使刚体绕某一点转动的效应由力对点的矩度量。力可以对空间任意一点取矩，矩心和力所决定的平面可以有任意方位，所以空间力对任一点的矩应该表示成矢量。

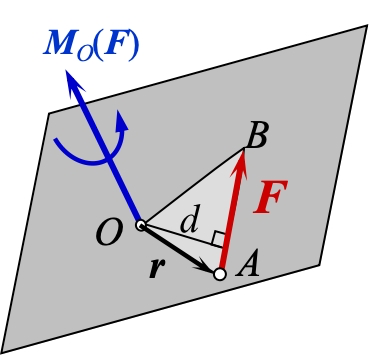
规定力矩矢符号为，力矩矢是一个定位矢量，它的大小和方向都与作用点的位置有关。

(2) 力对点之矩的矢积表达式

即力对点的矩矢等于矩心到该力作用点的矢径与该力的矢量积。

(3) 力对点之矩的解析表达式

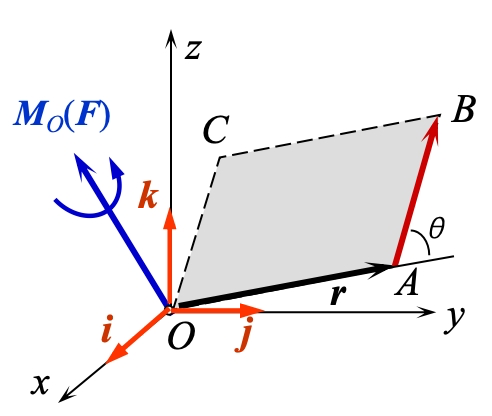
证明：

把上两式代入得：

2、力对轴的矩

(1) 力对轴之矩的定义

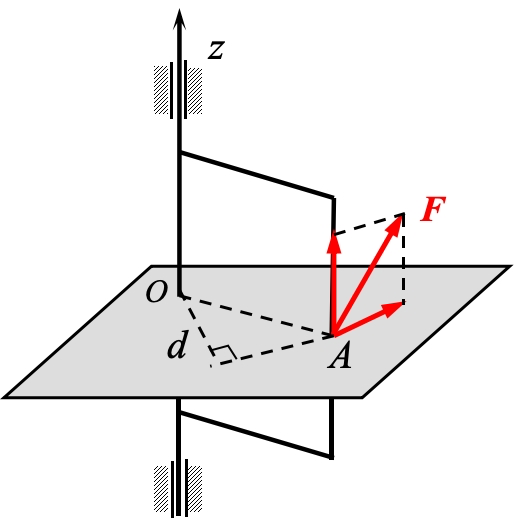
力对轴的矩用来量度力使所作用刚体绕轴转动的效应。

(2) 力对轴之矩的矢积表达式

把力的大小与其作用线到轴的垂直距离的乘积加以适当的正负号，有：

即力对任一轴的矩等于此力在该轴的垂直面上的投影对投影面和该轴交点的矩。那么，关于力对轴之矩存在下面几种特殊情况：

1. 力和轴平行，即，力对轴的矩等于。
2. 力的作用线通过该轴，即，力对轴的矩等于。

(3) 力对轴之矩的解析表达式

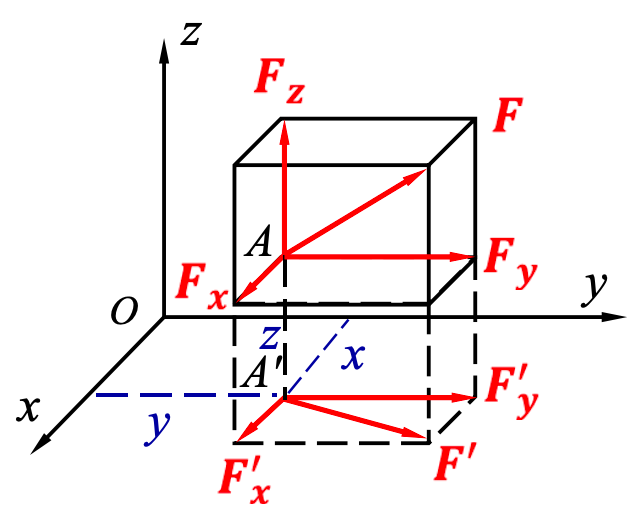
以表示力作用点的坐标，、、表示力在各坐标轴上的投影，力对轴的矩为：

同样地，可以得到：

3、力矩关系定理

力对坐标轴轴的矩的解析表达式为：

力对原点的矩的解析表达式为：

比较可得：

所以，力对坐标原点的矩在各坐标轴上的投影，等于该力对相应坐标轴的矩。反过来，若已知力对坐标轴的矩，则反过来可以求得对原点的矩的大小：

和方向余弦：

二、任意力系的简化和合成

1、力线平移定理

把力作用线向某点平移时，必须附加一个力偶，此附加力偶矩矢等于原力对点的矩矢。

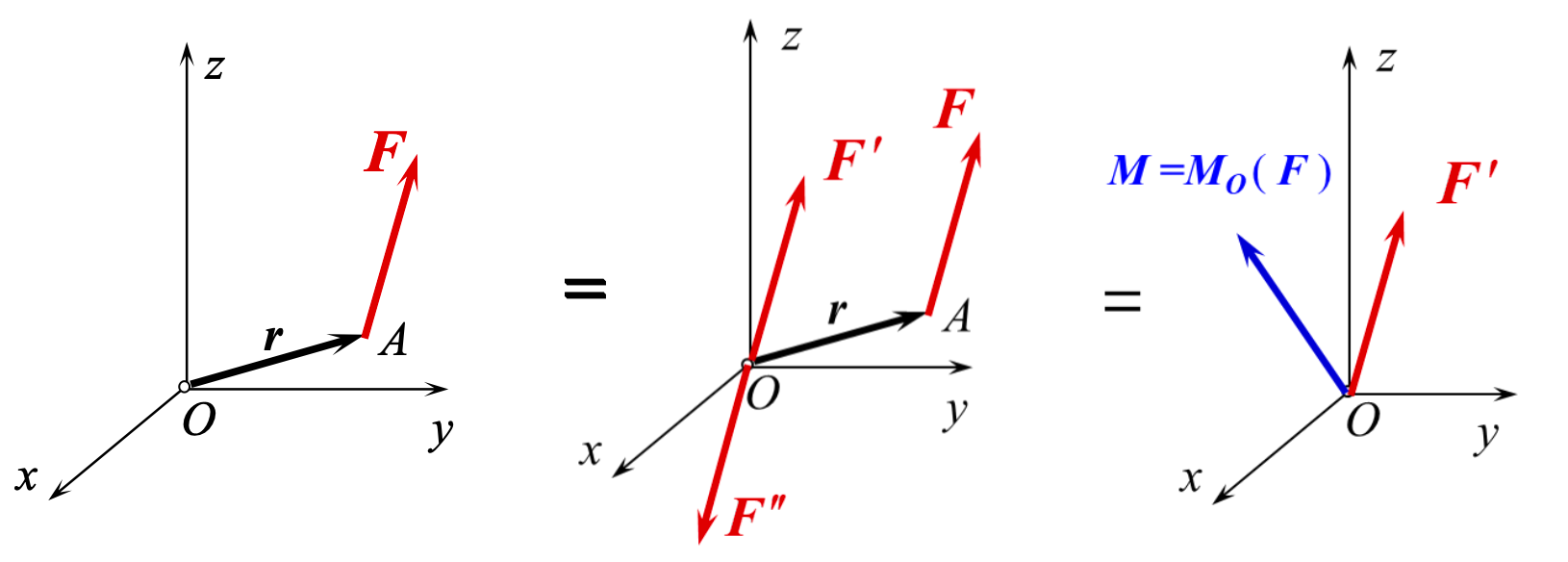
上图利用加减平衡力系定理说明这个问题。其中

2、任意力系的简化

(1) 空间任意力系的简化

空间任意力系向任一点简化后，得到一个空间共点力系和一个空间力偶系。并将他们合成。

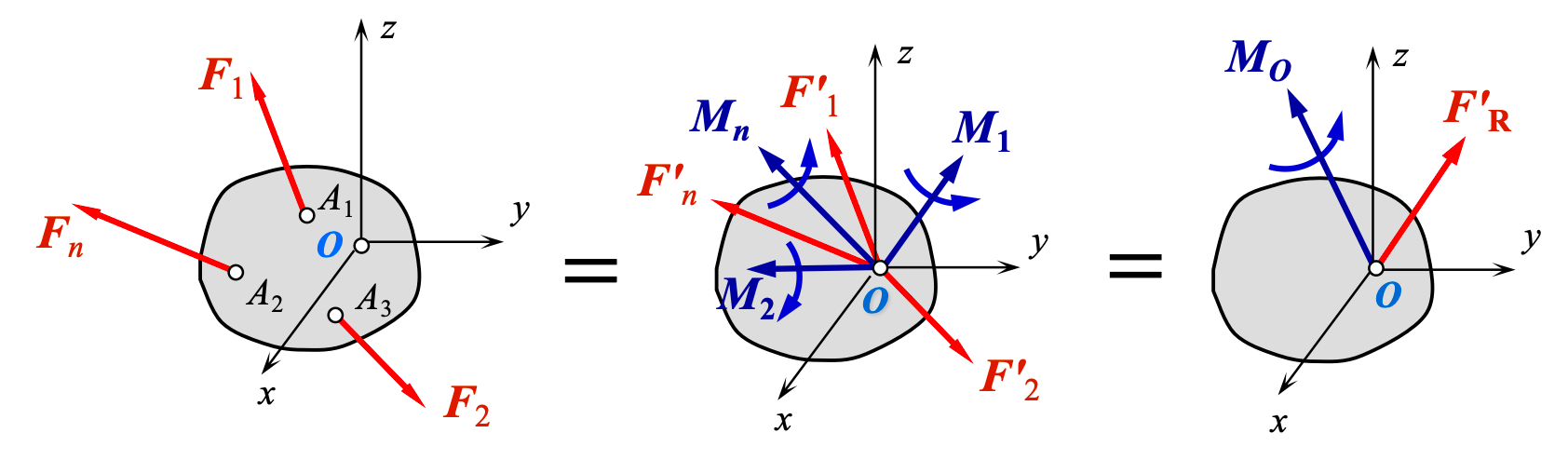
共点力系的合成结果为一作用在点的力。这个力称为原空间任意力系的主矢。

附加力偶系的合成结果是一个力偶，此力偶的矩矢用代表，称为原空间任意力系对简化中心的主矩。

由此得出结论：空间任意力系对简化中心的主矢为：，主矩为：。空间任意力系向任一点简化后，一般得到一个力和一个力偶。这个力称为原力系的主矢，它等于力系中所有各力的矢量和，作用在简化中心，它与简化中心的位置无关。这个力偶称为该力系简化中心的主矩，它等于力系中所有各力对该简化中心的矩之矢量和，主矩则一般与简化中心的位置有关。

(2) 主矢与主矩的计算

主矢在直角坐标系的投影：

主矢的大小和方向余弦：

主矩计算通常用解析法，且考虑到空间力对点的矩与力对过该点的轴的关系，把空间力对点的矩的矢量计算转换为对轴的代数计算：

(3) 平面任意力系的简化

对于平面任意力系的简化，可参考空间任意力系的简化过程进行，注意到在平面中将力偶的矩定义为代数量，得到以下结论：平面任意力系向作用面内任一点简化的结果，是一个力和一个力偶。这个力作用在简化中心，它的力矢等于原力系中各力的矢量和，并称为原力系的主矢。这个力偶的矩等于各附加力偶矩的代数和，它称为原力系对简化中心的主矩，并在数值上等于原力系中各力对简化中心的力矩的代数和。

(4) 补充：固定端（插入端）约束¹

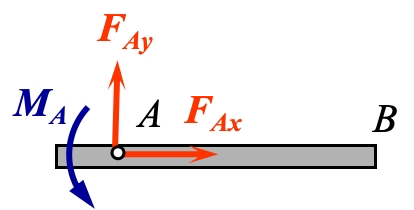
上图为固定端约束示意图。

3、任意力系的合成结果

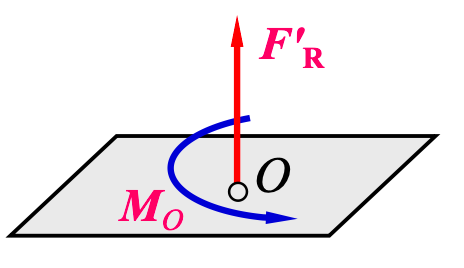
(1) 力系合成为合力偶

，而，则原力系合成为一个矩矢为的合力偶。该力系的主矩不随简化中心的位置而改变。

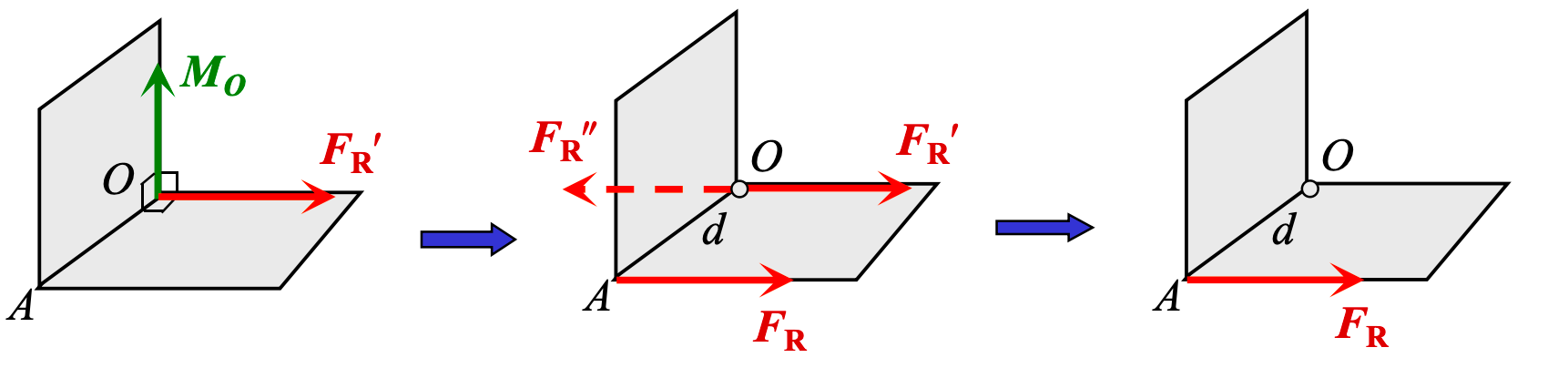
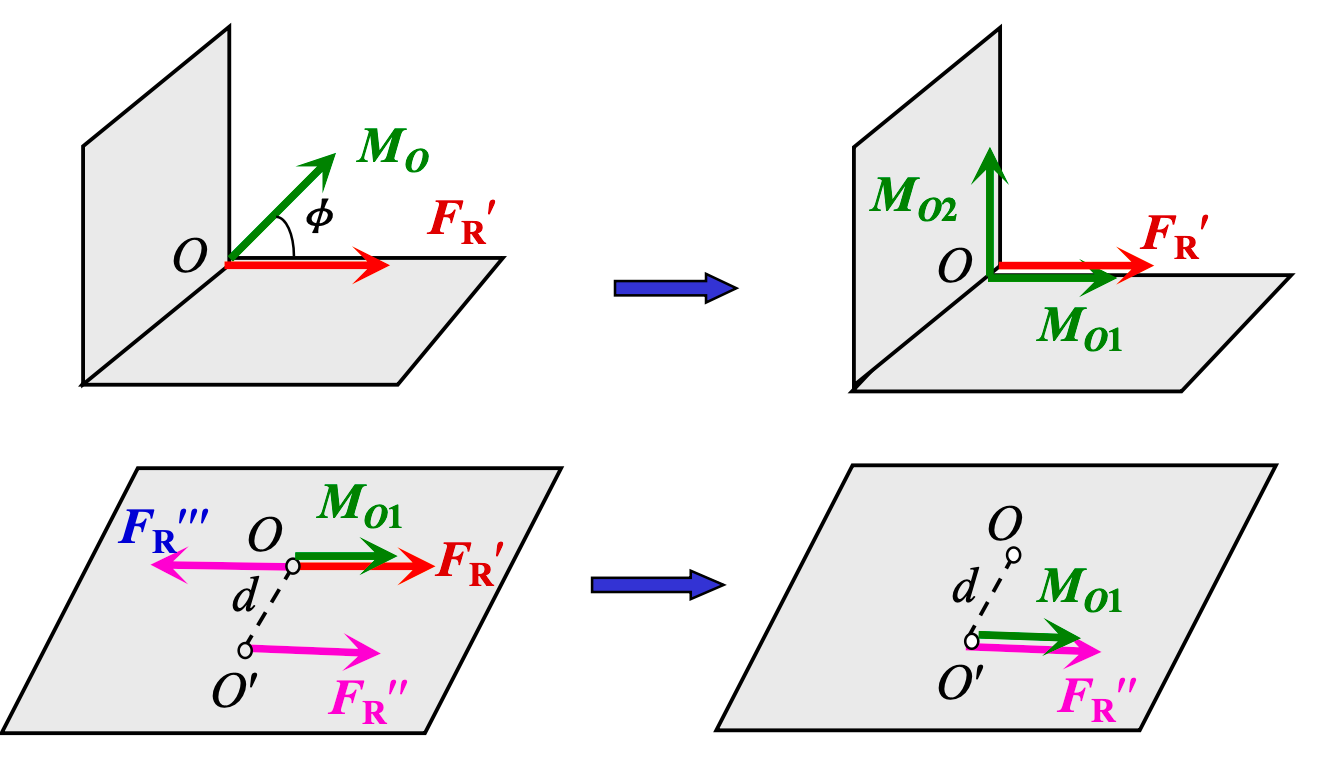
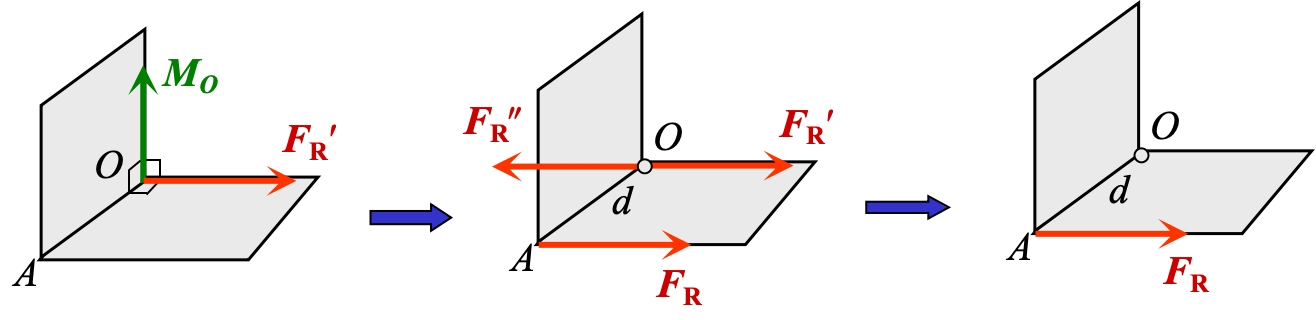
(2) 力系合成为合力

1. ，则原力系合成为一个作用于简化中心的合力，且。

2. ，且。则原力系仍然合成为一个合力。方法如下图：

   

(3) 力系合成为力螺旋

，且 ，力系合成为一个力（作用于简化中心）和一个力偶，且这个力垂直于这个力偶的作用面。这样的一个力和一个力偶的组合称为力螺旋。下图是一个右手螺旋，即力矢与力偶矩矢指向相同。

,且与成任意角，力系合成为一个力螺旋。

4、合力矩定理

在空间任意力系（）的合力为的情况下，有，根据主矩的定义

即：

1. 力系如有合力，则合力对任一点的矩等于力系中各力对同一点的矩的矢量和。
2. 力系如有合力，则合力对任一轴的矩等于力系中各力对同一轴的矩的代数和。

三、任意力系的平衡条件和平衡方程

1、空间任意力系平衡的充要条件

力系中所有各力的矢量和等于零，以及这些力对任何一点的矩的矢量和也等于零。在空间中，三个方向上的合力为零，力矩也为零，即为平衡。

2、空间平行力系平衡的充要条件

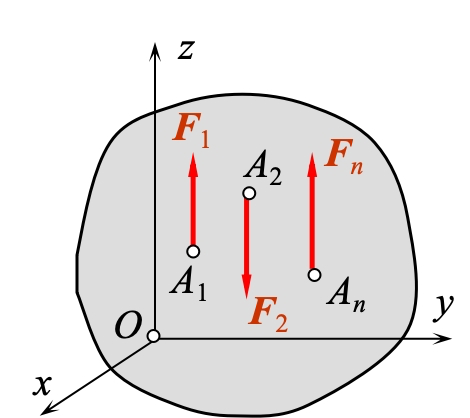
上图所示，为一个空间平行力系，其中存在：

所以只需要满足：

所以，空间平行力系平衡的充要条件是：力系中的各力在与其作用线平行的轴上的投影的代数和等于零，以及这些力对于任何两条与其垂直的轴的矩的代数和也分别等于零。

3、平面任意力系的平衡方程

平面任意力系可以看做是空间任意力系的特殊情况，其自身满足：

所以只需要：

平面任意力系平衡方程的充要条件是：力系中的各力在其作用平面内两坐轴上的投影的代数和分别等于零，同时力系中的各力对任一点的矩的代数和也等于零。

平面任意力系平衡方程也存在其他形式：

1. 二矩式：

   要求两点的连线不和轴相垂直。如果平面上的力对点的力矩同时为零，必须要求所有力的合力沿着连线方向，而不与轴垂直，所以可以说明，且。

2. 三矩式：

   要求三者不共线。推导方式同上。

4、平面平行力系的平衡方程

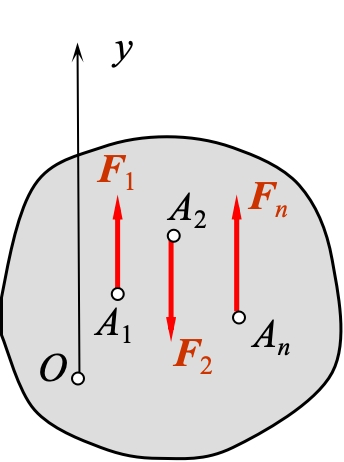
上图所示，为一个平面平行力系，其中存在：

所以还需要满足：

平面平行力系平衡的充要条件：力系中的各力的代数和等于零，同时这些力对任一点矩的代数和也等于零。

四、静定与静不定问题的概念

1、相关概念

• 物体系平衡方程的数目：由个物体组成的物体系，总共有不多于个独立的平衡方程。
• 静定问题：当系统中未知量数目等于或少于独立平衡方程数目时的问题。
• 静不定问题：当系统中未知量数目多于独立平衡方程数目时，不能求出全部未知量的问题。