一、复变函数的积分

1、复变函数积分的定义

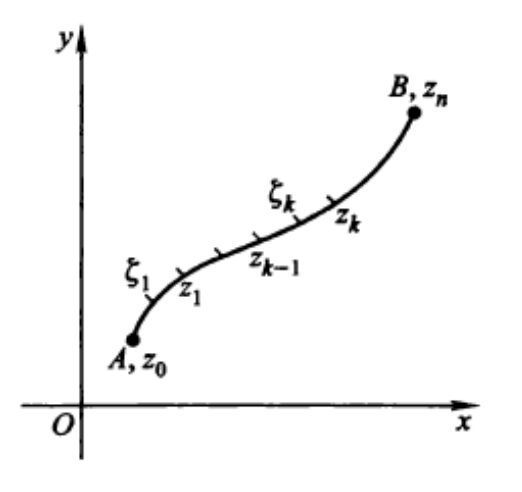
给定一个复变函数以及复平面上的一条光滑的曲线。我们把光滑的曲线分成段（不一定是均分），其中个点的坐标分别为：

在第 个分段上任意取一点，进行如下的求和：

当分段数量，且每个分段对应的（实际上是该段的长度），如果上面求和极限存在， 且该极限的值与的取值方式无关，那么我们称该极限就是复变函数沿着曲线的路径积分，记作：

2、复变积分的计算方法

考虑到

可以把上面积分表示为：

也就是说，复变函数的路径积分可以归结为几个实变函数的线积分（第二类线积分）。因此实变函数中线积分的一些性质对于复变函数的路径积分同样成立。

二、柯西定理

对于一般的复变函数，其积分值不仅依赖于起点和终点，还有可能与积分的具体路径有关。沿着不同积分路径的积分可能不尽相同。联系微积分的相关知识，寻找积分与路径无关的复变函数的特点。¹

1、单连通区域柯西定理

如果复变函数在闭的单连通区域上是解析，则沿上任意一段简单的光滑闭合曲线（这里简单指曲线不交叉，围成一个单连通区域）有积分关系：

证明： 是简单的封闭曲线，在其所围成单连通区域上有格林公式：

复变函数的积分可以化为：

包含两个实变函数的线积分，由于在上解析，因而在上连续，而且满足柯西-黎曼方程

所以可以将原式进行变形：

2、多连通区域柯西定理

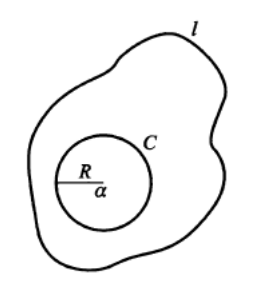
有时侯，复变函数在区域上并非是处处解析，在某些点或者某些子区域上不可导（甚至不连续或根本没有定义，我们称这样不解析的点为奇点）。为了应用柯西定理，我们需要去掉这些奇点附近的区域（挖去一个大小合适的孔洞），来构造一个多连通区域，使得该复变函数在此多连通区域内是解析的。（可以联想微积分中的绕洞积分）

多连通区域柯西定理：如果是闭多连通区域上的单值解析函数，那么在多连通区域的边界上有：

式中为区域外边线，为区域的第条内边界线，所有积分均沿着边界线的正方向进行。（外边界：逆时针方向，内边界：顺时针方向）

证明：

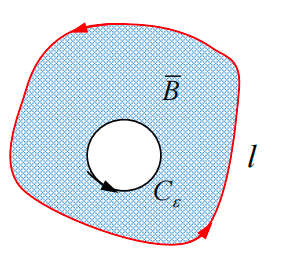
和多连通区域上格林公式的证明相同，我们在多连通区域上进行开槽， 把多连通区域转化为一个单联通区域。根据 在此单联通区域上，复变函数是解析， 所以沿此单联通区域边界的路径积分为零。显然在开槽附近两条直线上的线积分由于走向相反，正好抵消。如果把内边界换成逆时针方向，那么内外边界的积分值相同。

三、复变函数的不定积分

根据柯西定理，如果复变函数在单连通区域上是解析，那么沿B上任何一路径的积分只与起点和终点的位置有关，而与路径的具体走向无关（沿封闭曲线的积分为零）。因此，当起点固定后，可以定义一个单值的不定积分：

可以证明，上述定义的不定积分在上也是解析，且，称 是 的一个原函数。

例：计算积分。是复平面的任意一点，，为任意一条封闭曲线。

解：

如果不在所围成的区域中，那么被积函数是解析的，根据柯西定理，积分值为零。如果位于所围成的区域内时，可以分成下面两种情况：

1. 如果,那么被积函数在所围成的区域上依旧是解析的，积分值也为零。

2. 如果 ,那么被积函数在所围成的区域中有一个奇点,复变函数不解析。

   

对于第二种情况，我们以点为圆心，在所围成的区域内作一个圆（其半径为）圆的边界为 。显然，复变函数 在挖去了圆的区域（由和所围成的区域）上是解析的，根据柯西定理，函数 在沿圆周上的积分和沿封闭曲线的积分是相同。我们可以用沿圆周的积分来代替。

在圆周C上:

如果 ：

如果 ：

最终得到：

从这个例子我们可以看到，当被积函数不是解析（有奇点）时, 我们可以构造挖去奇点的圆形区域, 根据柯西定理, 用圆形区域边界的积分来代替。

四、柯西积分公式

1、单连通区域上的柯西积分公式

如果在闭单连通区域上解析，为边界，，则有柯西积分公式：

证明：根据前面例子所得到的结论，对于任意包含点 的简单封闭曲线,成立

因此有恒等关系：

所以只需要证明：

即：

函数是解析，因此被积函数只有一个奇点。不妨以为圆心，任意小的为半径，作一个小圆，记圆的边界。显然在与所围成的复连通区域上被积函数是单值解析，根据柯西定理，沿积分和沿的积分值应该是相等。

因此需要证明：

根据积分不等式：

由于是个连续函数，，只要半径 足够小，可以任意小。 也就是说当时，：

最终得到：

证毕

换一种表述，如果在闭的单连通区域上解析，那么，对于区域内任意一条包含的封闭曲线：

从柯西积分公式可以看到：在区域内的一个解析函数，当在区域边界上的函数值给定以后，根据柯西积分公式，区域内任意一点的函数值也就确定下来了。换个说法，如果两个解析函数在边界上的值相同，那么它们在区域内任意一点的函数值也相同。

2、多联通区域上的柯西积分公式

对于多连通区域上的解析函数，同样可以得到相应的柯西积分公式：

3、区域外部的柯西积分公式

设在闭回路的外部区域是解析，而且在无穷远处的函数值有限，那么 有下面的柯西积分公式：

这里要注意沿边界的积分方向，若沿曲线积分正方向，则需要添加负号。

4、高阶导数柯西公式

如果在封闭曲线内解析，那么对于封闭曲线内的任意点，有柯西积分公式：

由于 不在曲线上，，所以右边积分表达式中被积函数可以求导，两边对求导数得到

更进一步，还可以继续进行求导，得到更为高阶的导数：

由此可以得出定理：解析函数可以求任意次导数，而且其任意次导数依旧是解析的。而实函数没有这个性质。

5、柯西型积分的解析性定理

若是区域内任意的连续函数， 是任意一条曲线（可以不闭合），对于区域内不在曲线上的任意点，定义：

可以证明这样定义的函数是解析的，而且：

6、柯西积分公式的一般形式及其变形

柯西积分公式的一般形式：是简单封闭曲线区域内任意的解析函数，对于区域内不在曲线上的任意点：

也可以变形为：

可用来求函数的围道积分。

例：求积分：

构造函数和变量：

使用柯西积分公式：

最后得到：

五、柯西公式扩展

1、柯西不等式

假设复变函数在圆形边界及其内部是解析，其在边界上的最大值为，那么有：

2、刘维尔定理

如果在全平面上为解析函数（全纯函数，整函数），并且是有界的，即，那么在整个复平面上必定是常数。

3、平均值定理

如果复变函数在圆形区域上解析，那么有：

也就是说，圆心处的函数值是圆周上函数值的算术平均。

4、模数定理

设复变函数在某个闭区域上为解析且不为常数，那么只能在区域的边界线上取到极大值。