复变函数论 - 老官童鞋gogo的博客

一、复数的基本概念

1、复数的表示

复数有三种表示方法：

代数表示：
三角表示：
指数表示：

三角表示与指数表示之间的转换利用到了欧拉公式：

上述表示方法中，为复数的模，为复数的辐角。在复平面上的表示为：

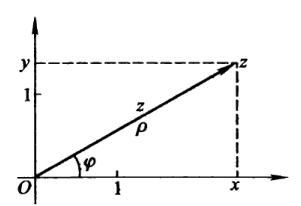
一个复数的辐角值不能唯一地确定，可以取无穷多个值，并且彼此相差的整数倍. 通常约定，以表示其中满足条件

的一个特定值，并称为的主值，或的主辐角。于是有：

复数“零”（即实部及虚部都等于零的复数）的辐角没有明确意义。

一个复数的共轭复数，指的是对应的点对实轴的反映，即

2、复数的运算

整数幂次定义：
平方运算：

前者是模的平方，等于复数与其共轭复数的成绩，后者为复数自乘。
整数根式：

需要注意：由于复数的辐角不是唯一，可以任意加减的整倍数而保持复数的值不变化，因此在上面的根式运算中，对应的辐角也就可以加减的整倍数。从而对于一个给定给定的复数，根式运算的结果可能不是唯一，而是有多个值与之相对应。

二、复变函数

1、复变函数的定义

若在复数平面（或球面）上存在一个点集（复数的集合），对于中的每个元素（每一个值），总有一个或多个复数值按一定的规律与之相对应，我们称为在复数域上的函数—复变函数，记作

称为函数的宗量（也称变量），为函数的定义域。

2、复变函数举例

多项式：（为正整数）
有理分式：（为正整数，式中的所有系数都是复常数）
根式：，要注意，这是个多值函数。
指数：
三角函数：

从而推导出以及。显然这里的三角函数与实数域三角函数有所不同，其取值的范围再不局限于到之间，但是函数的周期还是的整数倍。
双曲函数：

对数函数：

在上面的公式中，为复数域，为实数域。二者区别很大。

幂函数：

幂函数可能是单值，也有可能是多值，取决于指数的值

3、复变函数的连续

若函数均连续，则复变函数连续。

4、复变函数的导数

(1) 复变函数导数的定义

设函数是在区域上的单值函数，对于上的某点，如果极限：

存在，并且该极限值与的方式无关，则称函数在点是可导，极限值称为函数在点的导数(或微商)，以或来表示。注意：复变函数导数定义在形式上跟实变函数导数定义相同，但复变函数可导的要求要严格得多：从复变函数导数的定义来看，作为复数，具有无数种方式，比如可以是（沿着复平面的实轴），可以是（沿着复平面的实虚轴），也可以是。要求其导数存在，上述极限就应该与的方式无关，也就是说，在复平面上沿不同方向所求得的极限具有相同值。

(2)导数的两种特殊情形

沿着复平面的实轴方向逼近，即：
沿着复平面的虚轴方向逼近，即：

(3)柯西-黎曼方程（C-R方程）

前面已经推导了导数的两种特殊情形，类比二元函数、全微分方程的相关知识，我们可以类比得出复变函数可导的必要条件，如果函数在点可导，则上面两种特殊极限必须存在并且相等，即：

上式即为柯西-黎曼方程，不满足柯西-黎曼方程的复变函数肯定不可导，满足柯西-黎曼方程的复变函数不一定可导。

当然，在极坐标系中也存在柯西-黎曼方程：

存在下面两种证明思路：

在极坐标系中，比较沿径向逼近零（）和沿周向逼近零，即（）两种情形下的极限，就得到极坐标系中的柯西-黎曼方程。

从直角坐标系中的柯西–黎曼方程出发，按照变换公式：

变换到极坐标系，也可得到极坐标系中的柯西–黎曼方程。

(4)复变函数可导的充分必要条件

函数可导的充分必要条件是，函数的偏导数存在且连续，并且满足柯西-黎曼方程。

证明充分性：

由于偏导数连续，对于二元的实函数和，我们可以分别对它们进行泰勒展开，相应的增量为：

当和时，。

假如和满足柯西-黎曼方程：全部化成关于的偏导数：

可以全部化成关于或的偏导数：

(5)复变函数的求导法则

一般情况下，复变函数的求导法则与实变函数的求导法则相同。

三、解析函数

1、解析函数的定义

如果复变函数在点的邻域上可以处处求导，我们称复变函数在点是解析的。更进一步，如果复变函数在区域上的每一点都是解析，我们称复变函数是区域上的解析函数。

需要注意的是，有些复变函数可能在某一点可导，但在这个点邻域的其他点是不可导的，如，在是可导，但在其他点是不可导，从而该函数不是解析的。所以解析性要求比可导性要求来得苛刻。

2、解析函数的特殊性质

(1)解析函数实部与虚部的正交性

如果复变函数在区域上是解析的，那么，（为常数）代表区域上的两组正交曲线族。

证明：

如果函数是解析，那么满足柯西黎曼条件：

等值线在某点的梯度方向为：等值线在某点的梯度方向为：
$这两族等值线的梯度是正交，表明曲线族也是正交。$

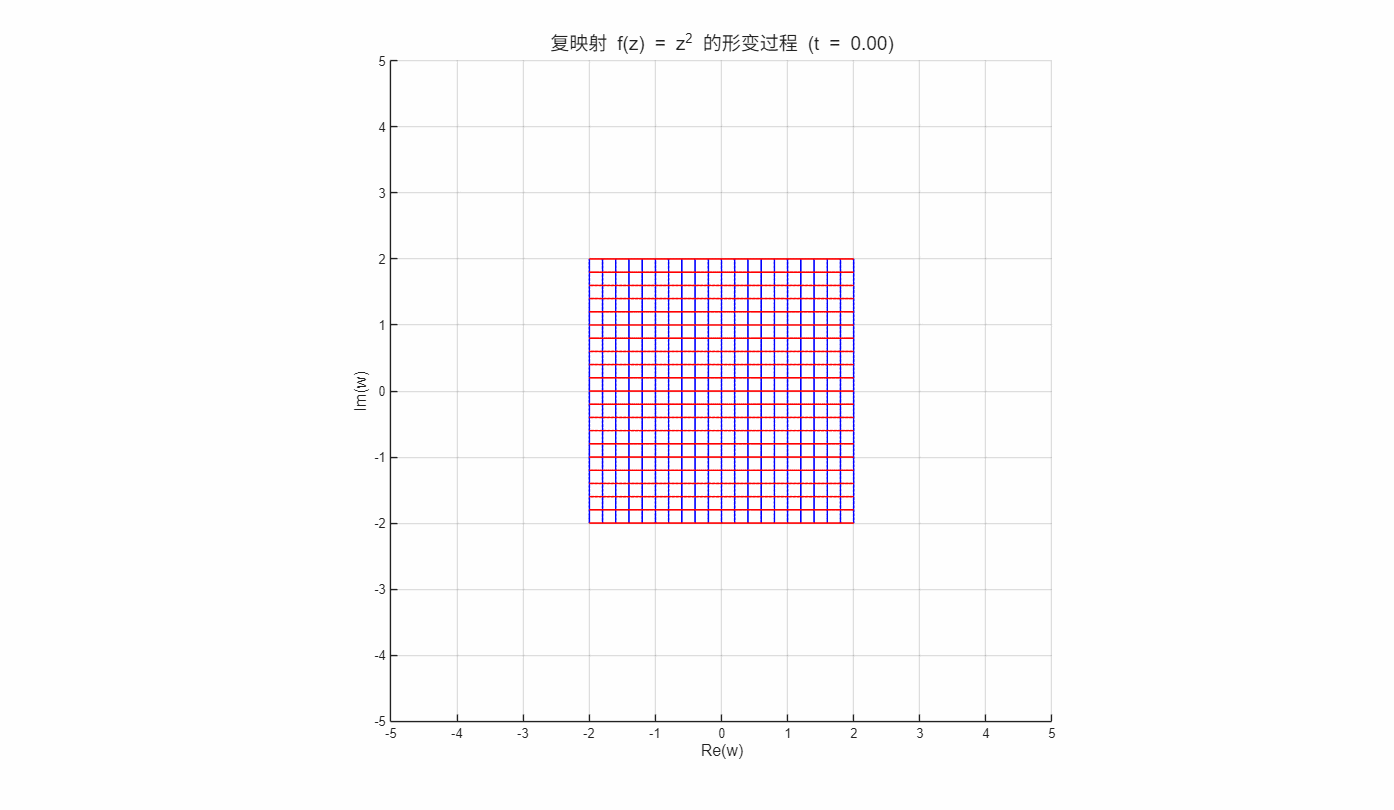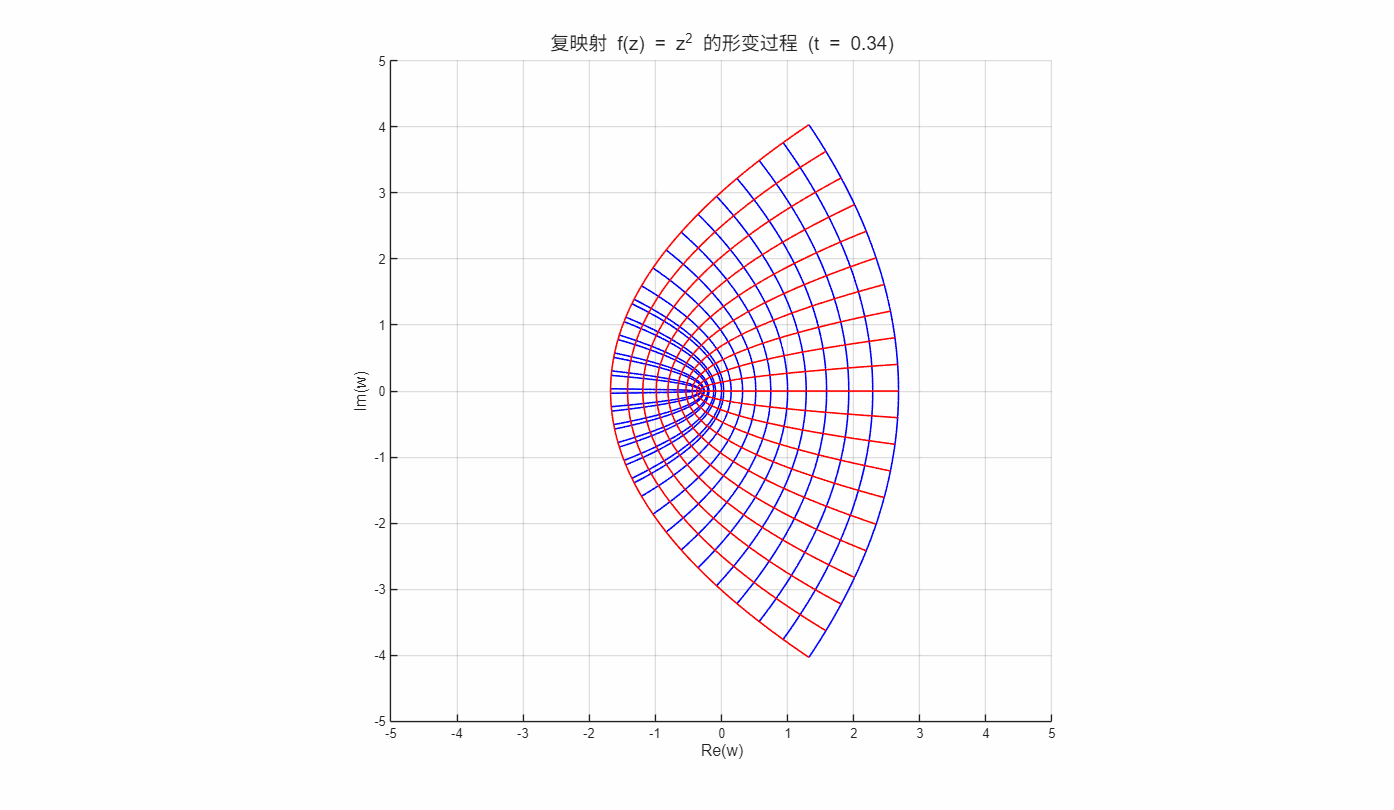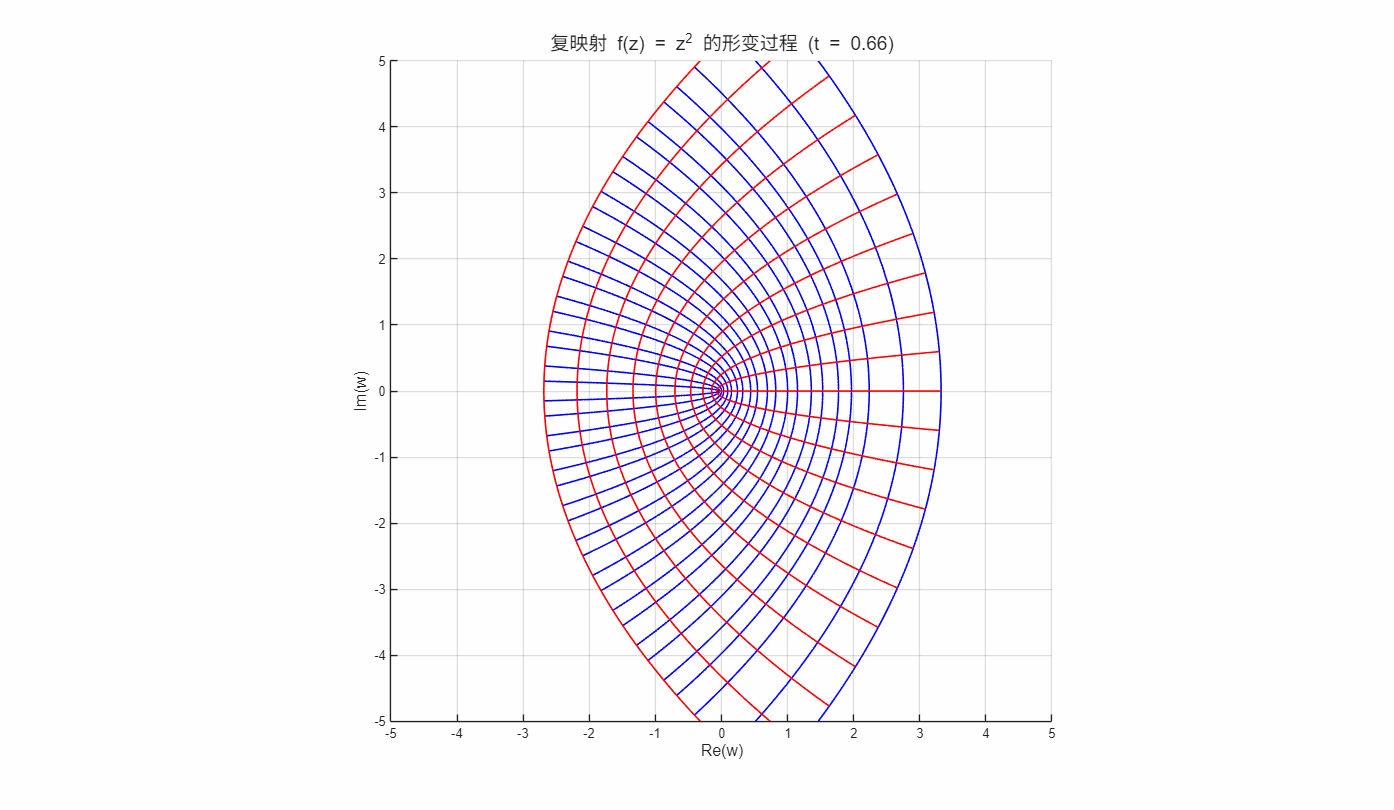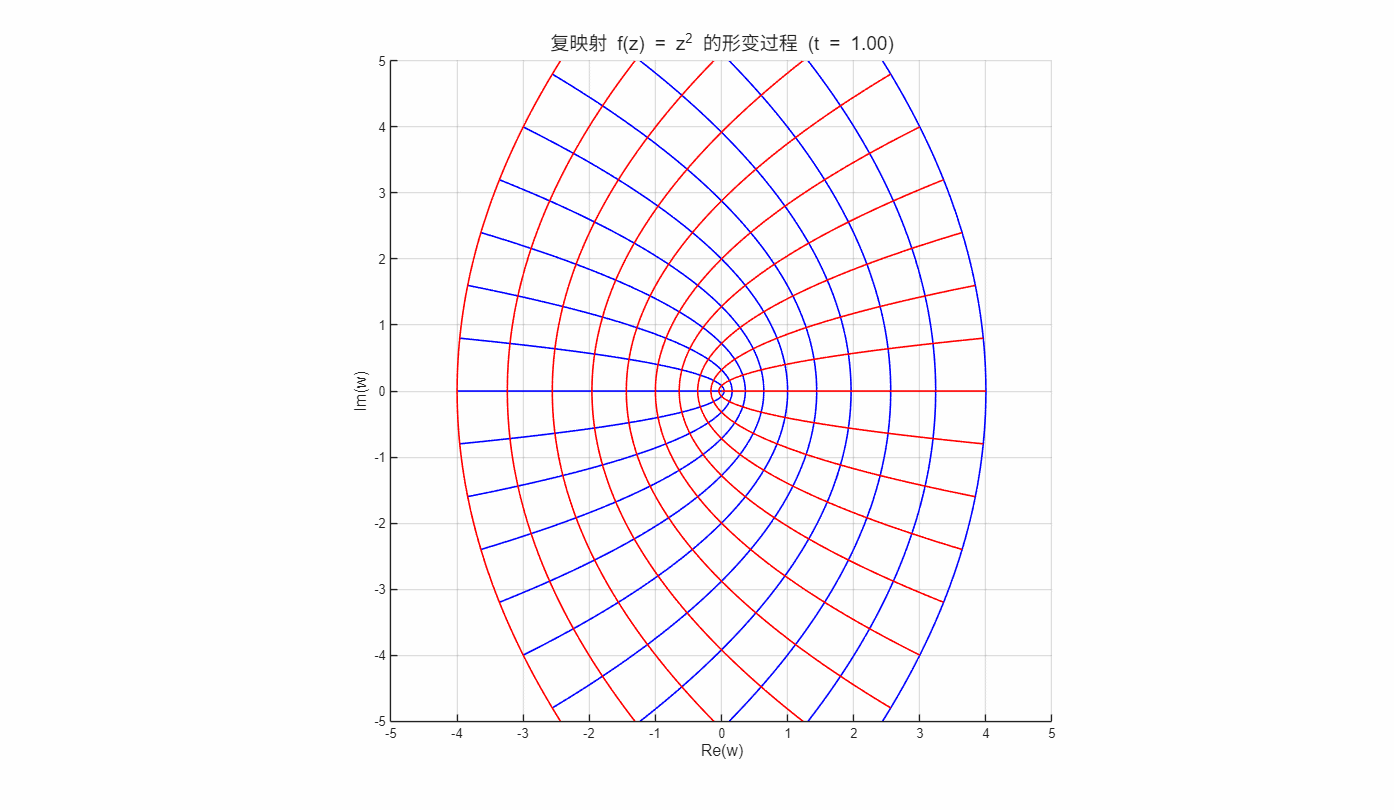
如上面动图所演示函数，在初始状态下时，红线和蓝线分别表示的等值线，经过变化后，红线和蓝线仍然保持正交。

(2)调和函数

在平面区域上, 如果一个函数具有连续的二阶偏导数，且满足拉普拉斯方程：

如果函数在区域上解析, 则其实部和虚部均为上的调和函数。

证明：

我们在后续=将会证明，某个区域上的解析函数在该区域上存在任意阶的导数。因此和的二阶偏导数存在且是连续的。根据解析函数的柯西-黎曼条件：

因此，函数是个调和函数。同理，函数也是个调和函数。我们把这样的一组调和函数统称为共轭调和函数。

给定了平面上的一个调和函数，如何求得与其共扼调和函数；或者说给定了某个解析函数的实部(或虚部)后，如何利用柯西–黎曼条件来确定这个解析函数？

不失一般性，假设解析函数的实部已经确定，那么的微分表达式为：

根据柯西-黎曼方程，可以写成：

这是一个全微分表达式，我们可以利用全微分方程的求解方法来解决这个问题¹

例：

已知解析函数的虚部，求实部和这个解析函数。

解：

在直角坐标中求偏导数和比较繁琐，直观的分析，改用极坐标可能会方便一点：

根据极坐标下的柯西-黎曼方程：

极坐标下全微分表达式为：

两边积分得到：

最后得到解析函数：

四、平面标量场

恒定场（稳态场）：如果物理场（电磁场、声场、温度场等）与时间无关，只与空间位置有关，我们称之为稳态场。
平面场：如果物理场沿空间某方向保持不变或者是均匀分布，我们只需要研究物理场在与该方向相垂直的平面上的变化规律，称之为平面物理场。

例：在没有电荷分布的区域，根据高斯定理，静电场的电势满足二维拉普拉斯方程，所以其电势可以视为某一解析函数的实部或虚部。把平面静电场的电势进行扩充到复空间中，用解析函数来表示该平面静电场的复势，该解析函数的实部或者虚部是实际问题的电势。

不妨取设为静电势（一般情况下都是取电势为实部），曲线族“ $常数$ ”为等势线族。接下来我们来看看具有什么物理含义。在平面上任取两点和，以及连接和的任一曲线，我们来计算通过该曲线单位高度的电通量。

这样，在和两点值之差代表了电场穿过两点之间曲线的单位高度电场强度通量。因此称为通量函数。

对于液体的无旋流动、平面温度场等这类满足拉普拉斯方程的物理问题，都可以考虑使用解析函数求解。

五、多值函数

1、为什么会出现多值函数

前面提到，或者是多值函数，具有多个分支。下面我们以根式函数为例来介绍多值函数的性质。

则的主幅角有两个值，相应地，有两个分支：

2、支点

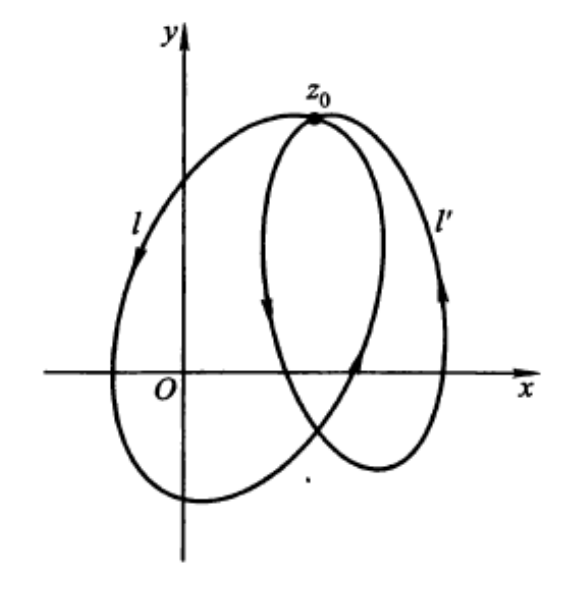
见上图，现在在复平面上取一个点，宗量从出发，沿着一条包含的闭合曲线回到（原来的点），转了一圈后增加了，显然从出发，又到达了，也就是说，明明是同一个位置，只是因为多在复平面上转了一圈，就从一个分支变为了领一个分支。所以不能看作是两个独立的单值函数。如果沿着不包含的闭合曲线回到，则转了一圈后，的值没有改变，一直留在一个分支中。

因此，对于多值函数来说，点具有这样的特征：当绕包含该点的曲线一周回到原来出发点时，对应的函数值将不再复原，从一个分支进入另一个分支，但是函数还是相同，我们称该点为多值函数的支点。更进一步，如果绕支点周后，函数值复原，回到原来的分支，我们称该点为多值函数的阶支点。对于函数 ,显然，当沿包含支点的曲线两周后，值将还原，因此，是的一阶支点。 $是$ 的一阶支点。对于函数,是二阶支点。

对于这样一个多值函数，我们进行如下分析：

上述函数的虚部，每一个对应着不同的函数值。因此，对于同样的，由于幅角的多值性，取对数后的函数值将有无穷多个，其黎曼面的分支也是无穷多个。显然，自变量绕原点一圈后函数值发生了改变，所以是的支点，同理，也是其另一个支点。

前面例子中，都提到了是一个支点，采取换元能够解决这个问题，使重新代回问题即可。

3、分支切割

因为多值函数在复平面上无法定义为单值解析函数。为了让函数在某一区域内单值，需要选择一个单值分支。这通常通过分支切割来实现，人为在复平面上去掉一条曲线，使得去掉后剩下的区域（称为分支面）上，函数变为单值。

以为例，首先将写作，，。于是

这时，只取在之间的那一值。我们人为从向正无穷延伸一条射线（通常选为负实轴或正实轴），把复平面切开。例如，沿正实轴（, ）作分支切割，则的幅角只取。切割后的复平面，去除了正实轴（含端点），在剩下的区域上，变成了单值函数。切割后，定义：

其中表示对数的主值。

当然，并不仅仅是负实轴、正实轴射线可以作为切割线，只要是将多个支点连接起来的线都可以分支切割，因为这样切割后无法找到一条闭合的含有支点的轨迹，使得从一个分支跨越到另一个分支，而正实轴、负实轴的射线，可以看作是连接支点和的一条线。

求解全微分方程的三种方法，参考文章：常微分方程求解（2） ↩

老官童鞋gogo