一、因果推理的基本概念

1、因果推理

哲学上把现象和现象之间那种“引起和被引起”的关系，叫做因果关系，其中引起某种现象产生的现象叫做原因，被某种现象引起的现象叫做结果。因果推理是一种重要的推理手段，是人类智能的重要组成。

2、辛普森悖论

辛普森悖论是统计学中的一种反直觉现象，指的是在分组数据中，某种趋势在各子组中都存在，但当把所有数据合并后，趋势却发生了逆转。例如，某药物在男性和女性两个子组都有提高治愈率的效果，但合并数据后可能反而显示总体治愈率下降。这是因为分组比例不同或其他潜在变量影响了整体结果。辛普森悖论提醒我们，在分析数据时，要注意分组情况和潜在的混杂因素，不能只看总体数据，否则可能得出错误的结论。

3、因果推理的主要模型

(1) 结构因果模型

结构因果模型（Structural Causal Model, SCM）是一种用来描述和分析因果关系的数学模型。它将真实世界中的变量及其因果关系用节点和有向边表示，通常使用有向无环图（DAG, Directed Acyclic Graph）。每个节点代表一个变量，每条有向边表示变量之间的直接因果影响。结构因果模型由三个要素组成：变量集合、结构方程（即每个变量如何由其他变量决定）和外生噪声变量。通过SCM，我们可以明确区分相关性和因果性，并能用“do运算”等方法计算干预的结果。结构因果模型广泛用于科学、经济学、人工智能等领域，用于推断因果效应、识别混淆变量和进行反事实分析。

结构因果模型由两组变量集合和以及一组函数f组成。其中，是根据模型中其他变量取值而给中每一个变量赋值的函数。如果变量出现在给变量赋值的函数中， 则是的直接原因。如果是的直接原因或者其他原因，均称是的原因。

中的变量被称为外生变量，即这些变量处于模型之外， 不对其阐述和解释；中的变量称为内生变量。以图中的节点来说明内生变量和外生变量的关系：每一个内生变量都至少是一个外生变量的后代；而每一个外生变量都不是其他外生或内生变量的后代，它们没有祖先，也就是说，外生变量都是图中的根节点。如果知道了每一个外生变量的值，就可以使用函数f来计算出每一个内生变量的值。

在结构因果模型框架下讨论某种治疗方案X对肝脏功能的因果关系。在讨论对的因果关系时，可能会假设肝脏功能Y会受到水污染的影响，由于水污染不会受到治疗方案X和肝脏功能Y的影响，因此，可将和作为内生变量，作为外生变量来进行研究。

每个结构因果模型都与一个因果图相对应。因果图中的节点是结构因果模型中U和V所包括的变量，节点之间的边表示函数。在中，若变量的函数包含了变量（的取值依赖于），则在中有一条从到的有向边。这里主要讨论因果图为有向无环图的结构因果模型。

(2) 因果图模型

在因果图中，若变量Y是另一个变量的孩子，则是的直接原因；若是的后代，则是的潜在原因。

(3) 因果图中联合概率分布

对于任意的有向无环图模型，模型中个变量的联合概率分布由每个节点与其父节点之间条件概率的乘积给出：

其中，表示节点的父节点集合（所有指向的节点）。这里包含了变量之间某种普遍成立的独立性假设。

对于一个简单的链式图，其联合概率分布可直接写成：

二、因果图结构

1、链结构

链是因果图的一种基本结构。它包含三个节点两条边，其中一条边由第一个节点指向第二个节点，另一条边由第二个节点指向第三个节点。

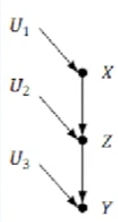
如上图，对于变量和，若和之间只有一条单向的路径，变量是截断该路径的集合中的任一变量，则在给定时，和条件独立。

2、分连结构

分连也是因果图的一种基本结构。它包含三个节点两条边，两条边分别由第一个节点指向第二个节点和第三个节点。

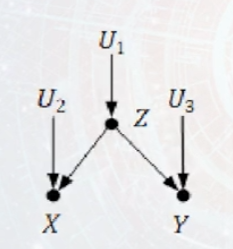
在分连结构中，给定时，和的联合概率：

即在分连图中，和在给定时条件独立。上式的第一步使用了条件概率的定义，第二步使用了乘积分解规则。

若变量是的共同原因，且到只有一条路经，则在给定时，条件独立。

3、汇连结构

汇连（又叫碰撞）也是因果图的一种基本结构。它包含三个节点两条边，两条边分别由第一个节点和第二个节点指向第三个节点。

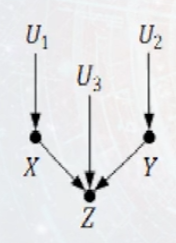
在汇连结构中，给定时，和的联合概率：

即在汇连图中，和在给定时条件相关。上式的第一步使用了条件概率的定义，第二步使用了乘积分解规则。

若变量是变量和的汇连节点，且到只有一条路径，则和相互独立，但在给定或的后代时，和是相关的。

4、D-分离

D-分离，可用于判断任意两个节点的相关性和独立性。若存在一条路径将这两个节点（直接）连通，则称这两个节点是有向连接的，即这两个节点是相关的；若不存在这样的路径将这两个节点连通，则这两个节点不是有向连接的，则称这两个节点是有向分离的，即这两个节点相互独立。

D-分离：路径被限定集阻塞当且仅当路径含有链结构或分连结构且中间节点在中，或路径含有汇连结构且汇连节点及其后代都不在中。若阻塞了节点和节点之间的每一条路径，则称给定时，和是D-分离，即给定时，和条件独立。

三、因果反事实模型

1、干预的因果模型

干预指的是固定系统中的变量，然后改变系统，观察其他变量的变化。

为了与自然取值时进行区分，在对进行干预时，引入“算子”，记作。

因此，表示的是当发现时，的概率；而表示的是对进行干预，固定其值为时，的概率。用统计学的术语来说，反映的是在取值为的个体上，的总体分布；而反映的是如果将每一个取值都固定为时，的总体分布。

以变量为条件是改变了看世界的角度，而干预则改变了世界本身。

2、因果效应差

因果效应差是指在其他条件相同的情况下，某个变量（通常是处理或干预变量）的不同取值对于结果变量的期望值造成的差异。它通常表示为，在设定某种干预和不干预时，结果变量之间的平均差值。而在设定某种干预的情况下变量产生的变化成为因果效应。

给定因果图，表示的父节点集合，则对的因果效应为:

3、反事实模型

反事实描述的是假设存在一个虚拟的平行世界，里面的所有因素与现实世界一模一样，两个相同的个体他和“他”分别在现实世界和平行世界中同时同地做了不同的选择， 现在他知道了现实世界中的结果，他想知道平行世界中的那个“他”的选择所带来的结果。然而，平行世界并不存在。幸运的是，反事实将告诉他另一个“他”的选择所带来的结果。

反事实计算的三个步骤：

1. 溯因：利用现有的证据确定环境

2. 动作：对模型进行修改，移除等式中的变量并将其替换为，得到修正模型

3. 预测：利用修正模型和环境计算反事实的值。