一、安培力

1、安培力推导

由安培定律：

以及毕奥-萨法尔定律：

将两式结合，可以得到安培力的表达式：

对于通电直导线来说，安培力可以直接写成：

2、安培力应用

(1) 两通电平行指导线的相互作用力

两根平行导线分别携带电流 和 ，相隔距离 。导线间的相互作用力由电磁场产生。

根据毕奥-萨伐尔定律，第一根导线在第二根导线位置处产生的磁场为：

第二根导线受到第一根导线产生的磁场作用，其微元段 受到磁力：

由于导线间的磁场与电流方向垂直，力的大小为：

将 的表达式代入：

将导线的长度单位化，磁力每单位长度为：

(3) 矩形线圈受到的安培力矩

一个矩形电流环处于均匀磁场 中，其电流 通过导线流动。电流环受到磁场的作用力，并产生一个力矩使其趋向于与磁场方向对齐。线圈电流产生的磁场对另外导线的作用力仅沿着导线框所在的平面，不产生力矩。

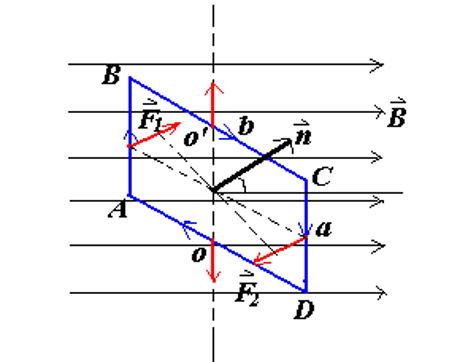
矩形电流环边长为 和 ，其四条边分别标记为 。磁力由磁场对每段导线施加的洛伦兹力产生：

对于垂直于磁场的边 和 ，电流方向与磁场方向垂直，因此磁力大小为：

力的方向根据右手定则，与纸面垂直（我感觉老师给的图中的方向错误了，不应该与线圈平面垂直）。

对于平行于磁场的边 和 ，电流方向与磁场方向平行，因此磁力为零：

磁力对矩形环的中心产生力矩 ，其大小为：

对于边 的力矩，力作用点距离环中心的垂直距离为 ，力矩大小为：

其中 是磁场 与环平面法向量 的夹角。

总力矩为两边力矩的加和（根据对称性直接得出另一边的力矩）：

化简得：

矩形环的面积为：

定义电流环的磁矩：

其中 是环平面的法向量，力矩可以写为：

(4) 任意形状的线圈受到的安培力矩

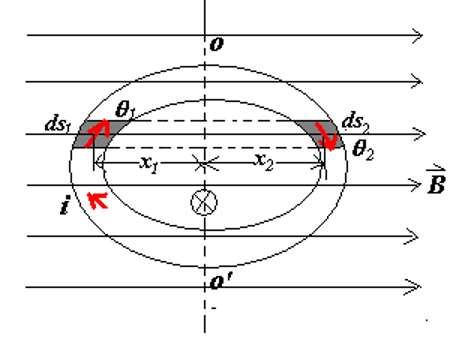
取沿着磁场方向取同一对称位置的微小线圈元，计算每一个微笑电流源的受力：

其中：

则：

计算力矩：

积分得到：

若，则

(5) 磁偶极矩的能量

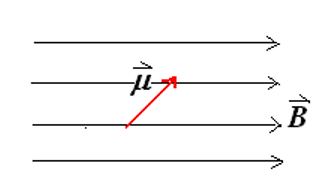
当时，得到：

二、洛伦兹力

1、洛伦兹力定义

洛伦兹力表示运动电荷在磁场中的受力，计算公式为：

在匀强磁场中电子做匀速圆周运动时，其周期为：

圆周运动半径为：

2、洛伦兹力与安培力

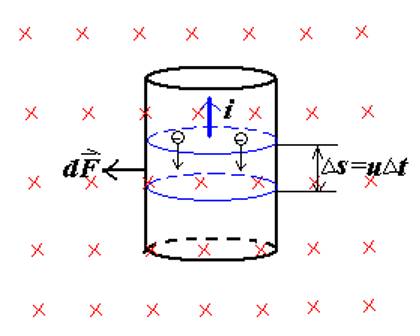
安培力可以由洛伦兹力推导而来，取微小长度的带电导线，电荷密度为，电荷运动速度为，在微小时间内，通过的电量为：

电流为：

将每一个电荷所受到的洛伦兹力求和：