一、安培定律

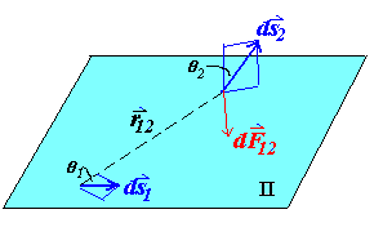
安培定律的核心在于描述电流之间的磁场与力的关系。具体来说，先是电流产生磁场，第一段导线上的电流会在其周围空间产生磁场（见下面的毕奥-萨伐尔定律），磁场方向由右手定则确定。然后磁场对第二段导线产生作用，第二段导线上的电流受到第一段导线产生的磁场的作用力。此力遵循洛伦兹力公式：

结合第一段导线产生的磁场表达式，可以推导出安培定律的形式。力的方向通过矢量叉乘确定，第一段导线的电流方向和指向第二段导线的单位矢量叉乘，确定磁场方向。第二段导线的电流方向 再与磁场方向叉乘，确定力的方向。整合上式，得到安培定律的计算式：

二、毕奥-萨伐尔定律

1、定律内容

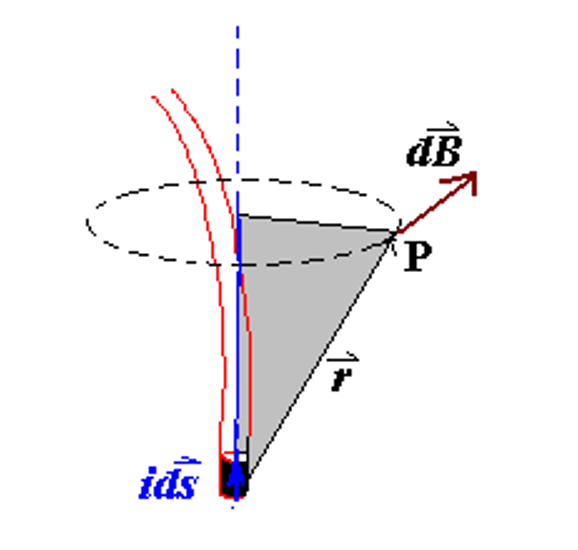
毕奥-萨伐尔定律是电磁学中的一个基本定律，用于描述电流元（微小段载流导线）产生的磁场。这一定律奠定了磁场与电流之间的关系。毕奥-萨伐尔定律的微分形式为：

其积分形式为：

3、毕奥-萨伐尔定律应用

(1) 带电直导线产生的磁场

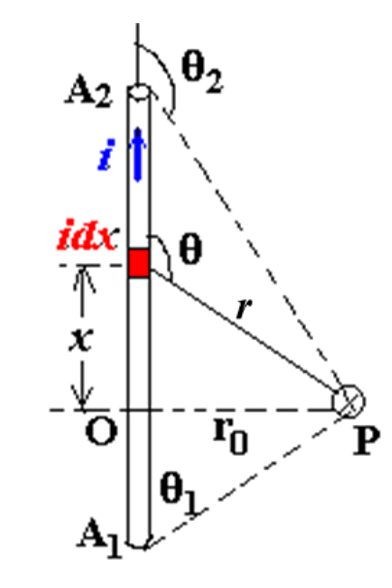
微元磁场公式

在点 处进行标量积分

结合几何关系：

坐标关系：

代入积分公式：

积分结果：

若导线为无限长，将，代入，可得无限长带电直导线产生的磁场：

(2) 带电圆环在轴向上产生的磁场

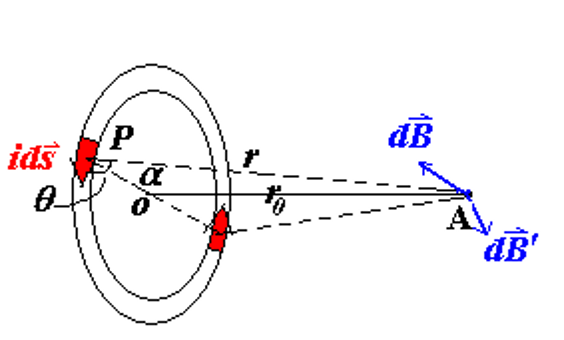
分量关系：

微元磁场大小：

几何关系：

磁场分量积分

代入公式：

环路周长为 ，积分后得到：

几何关系为：

最终磁场公式：

(3) 磁偶极矩定义

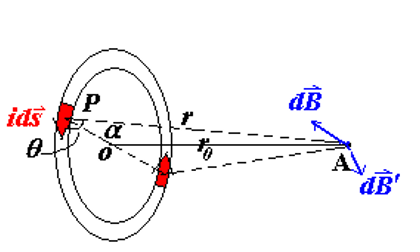
写出磁场表达式：

定义磁偶极矩：

代入后磁场公式：

对于 匝的线圈：

矢量形式磁偶极矩：

(4) 氢原子磁场和波尔磁子

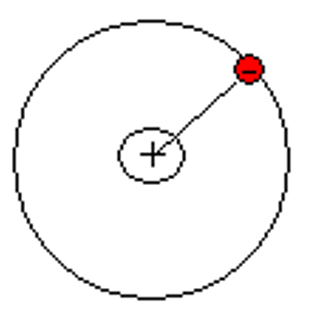
根据电流的微观定义：单位时间内流过某一横截面的电荷量。可以写出氢原子外围电子的电流，其中为电子绕原子核的运动频率：

氢原子电子的磁偶极子比较特殊，单独拿出，称为波尔磁子，是量子力学的一个基本单位。

(5) 无限长带电平板条在距离平板垂直平分线处的磁场强度

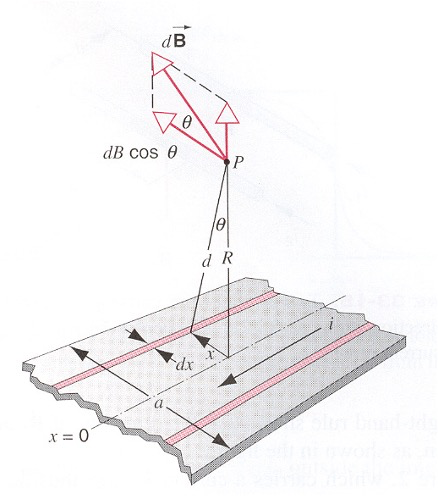
将平板分割为无穷多带点直线，使用前文所推导的公式，计算得：

由题目可知，在沿着平板条长度方向的磁场为，只需要计算垂直于平板条长度方向的磁场

化简积分得：

计算微元：

积分得出结果

在特殊情况下，若点远离条带：

可以将条带近似看做为直导线。

若点非常接近条带：

可以将条带近似看作为无限大通电平板。于是得到了水平方向上无限长通电平板产生的磁场。

(6) 螺旋管在管内轴向上产生的磁场

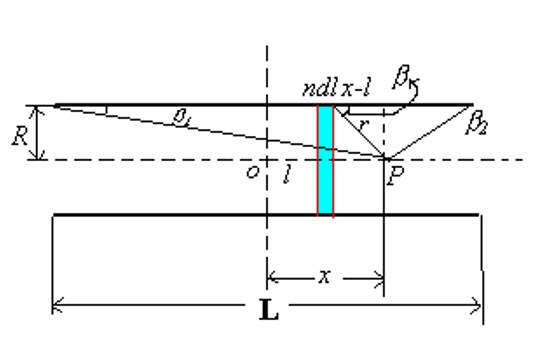
螺线管看作是非常多的细导线环的叠加，按照图示，微分形式的磁场表达式：

其中为单位长度线圈的匝数，总磁场可以积分得到：

其中：

进行积分化简：

根据几何得出特殊角度关系：

那么对于无穷长的螺线管，可以将代入，得到：

在无限长螺线管的一端，可以将，得到：

但是在现实生活中，螺线管并不一定是单层缠绕的，可能会在同一横截面缠绕一层很厚的线圈，例如：

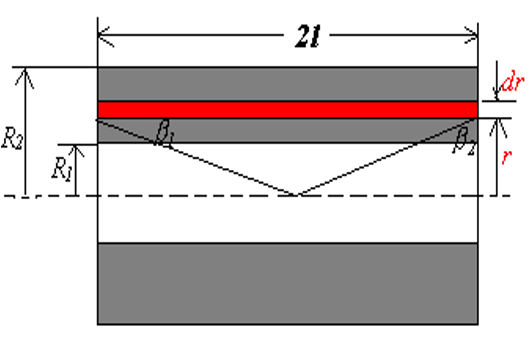
上述线圈的总匝数为，长度，厚度为，下面在螺线管的中心位置研究问题。将这种多层螺线管看成很多个单层螺线管叠加，其中表示的是单位面积的线圈匝数，有：

角度关系为：

代入到单层螺线管的表达式中：

总磁场：

通过积分结果：

三、磁场高斯定理

1、磁通量

磁通量定义为穿过某一给定表面的总磁场，单位为韦伯，其数学表达式为：

其中磁场矢量，为微小面积矢量，其方向垂直于表面，为磁场矢量与面积矢量的夹角。

2、磁场

磁场与磁通量密度的关系为：

3、磁场高斯定律

毕奥-萨伐尔定律描述了电流元对某点磁场的贡献：

对于微小区域，磁场的贡献为：

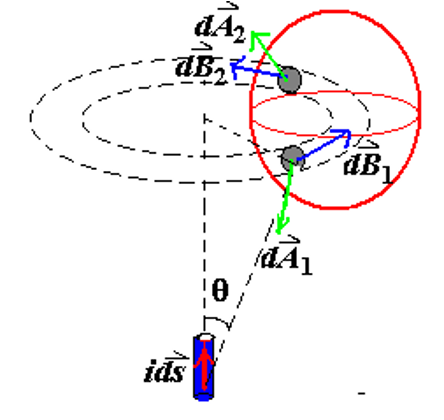
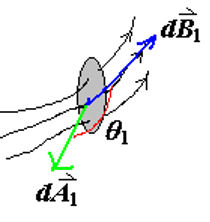
考虑一个闭合表面上的任意两个小区域 和 ，其磁通量分别为：

对于区域 ：

由于角度关系：

因此：

对于区域：

由于角度关系：

因此：

对于闭合曲面，区域和面积满足：

于是磁通量满足：

积分得到磁场的高斯定理：

磁场的高斯定律指出，穿过一个闭合表面的净磁通量始终为零，这意味着磁场线总是形成闭合回路，或者从无限远处延伸至无限远，没有起点或终点，因为自然界中不存在磁单极子。等价的微分形式为：

四、磁场安培环路定律

1、定律内容

安培环路定律描述了环路上的磁场与环路所包围的电流的关系，其数学表达式为：

其中，表示磁场矢量，为环路上的微小路径元，为真空磁导率，为环路所包围的总电流。电流的正负符号由右手定则决定，如果电流方向与右手定则一致，用正号，如果电流方向与右手定则不一致，用负号。

2、磁场安培环路定律应用

(1) 无限长直导线的磁场

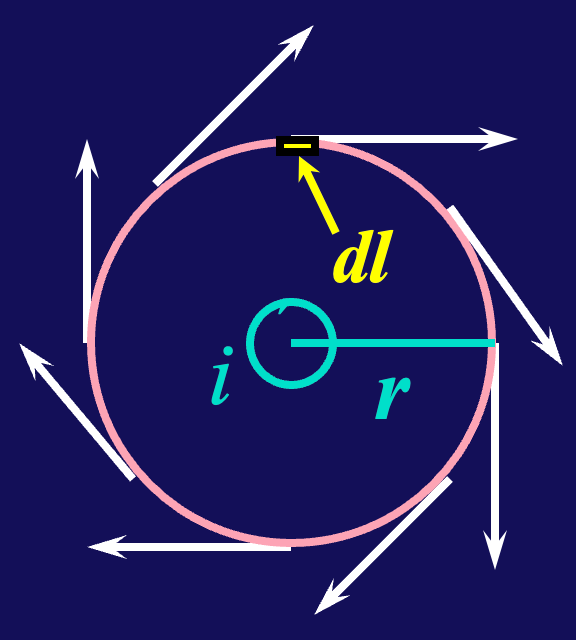
选择一个半径为的圆环作为积分路径，其中心位于导线轴上，且圆环位于垂直于导线的平面内。根据安培环路定理：

其中与的方向相同，得到：

移项得到：

(2) 长导线内部的磁场

对于一根半径为的长导线，导线内部具有均匀分布的电流。

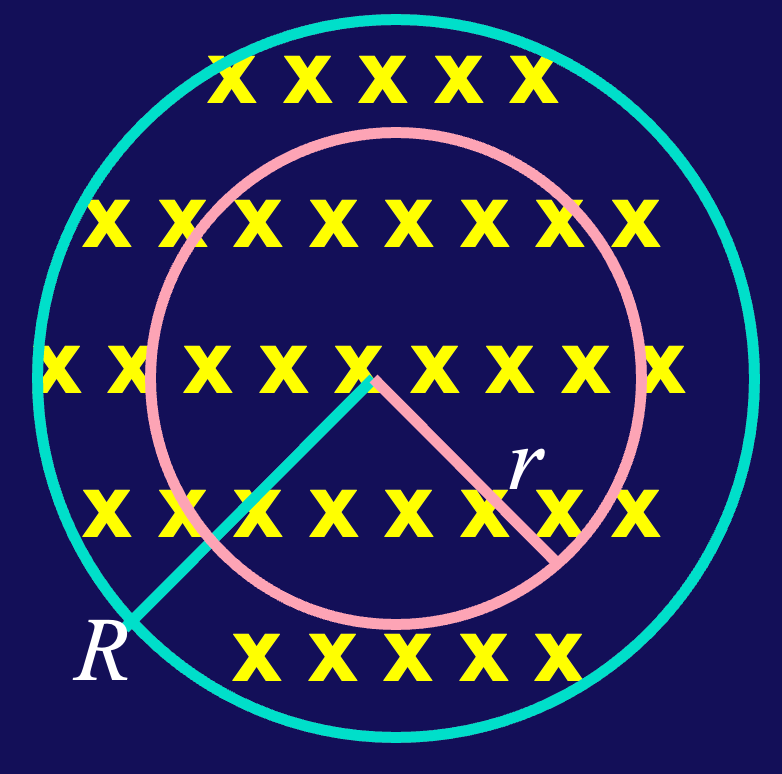
由于电流分布具有轴对称性，选择一个半径为 的圆环作为积分路径，其中心位于导线轴上，且圆环位于垂直于导线的平面内。根据安培环路定律：

对于选择的圆环路径，由于磁场 和路径方向 平行，点积简化为标量乘积：

环路的路径长度为圆周长 ，所以积分结果为：

因此，安培环路定律可写为：

导线内的电流均匀分布，电流密度为：

在半径为 的圆环内部，所包围的电流为：

将 代入安培环路定律：

解得磁场大小：

(3) 无穷大通电平板产生的磁场

一个无限大的电流面由一定密度的平行电流线组成，每单位长度包含 条电流线，每条电流线的电流为 。

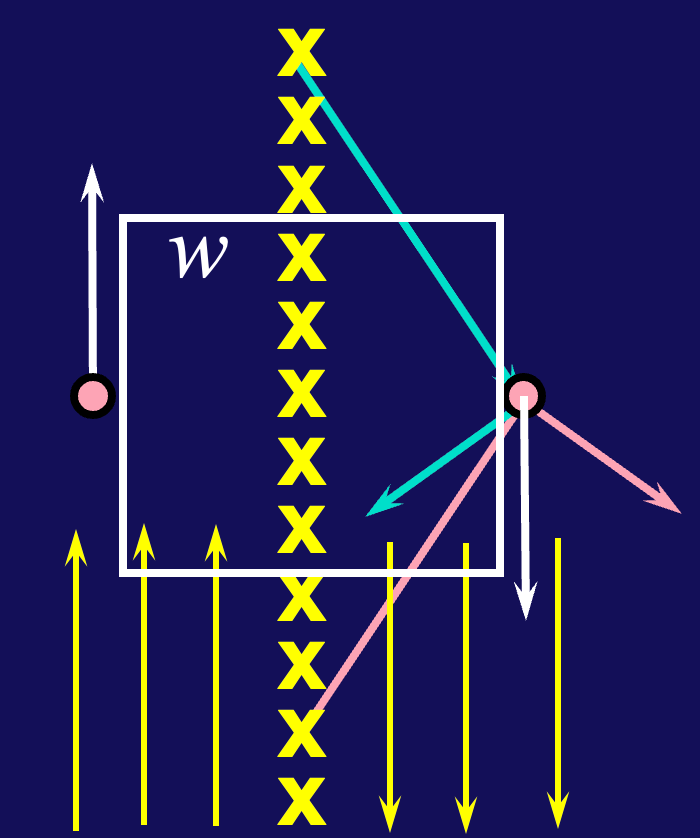
选择一个正方形环路，边长为 ，环路垂直于电流面，环路的两条垂直边磁场方向与路径方向垂直，因此磁场与路径的点积为零，环路的两条平行边磁场方向与路径方向平行，因此磁场贡献为标量。根据安培环路定律：

沿环路积分得到：

因此：

电流面中每单位长度包含 条电流线，每条电流线的电流为 ，所以总电流包围为：

将 代入安培环路定律：

解得磁场大小：

(4) 无限长螺线管的磁场

无限长螺线管由均匀分布的线圈组成，单位长度的线圈数为，电流沿线圈流动。

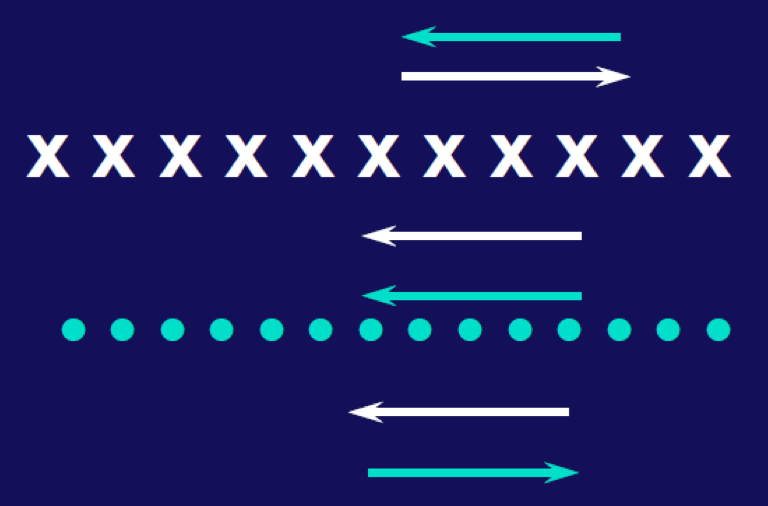
在无限长螺线管内部，选择一个正方形路径（边长为 ），其环路的一部分位于螺线管内部，另一部分位于螺线管外部。根据安培环路定律：

螺线管内部，磁场 平行于路径方向，且大小恒定：

螺线管外部，磁场为零（因为螺线管为无限长磁场从无限远处延伸至另一个无限远）：

环路其他段与磁场方向垂直，因此贡献为零。总积分结果：

螺线管内部包围的电流为：

将 代入安培环路定律：

解得螺线管内部的磁场大小：

(5) 螺绕环产生的磁场

螺环由 匝线圈组成，每匝电流为 ，线圈绕成环形，半径为。

由于螺环的对称性和闭合电流分布，螺环外部的磁场方向相反，导致磁场抵消。因此螺环外部的磁场为零：

为了计算螺环内部磁场，选择一个半径为 的圆形路径，圆心位于螺环的中心，圆形路径完全位于螺环内。根据安培环路定律：

沿圆形路径积分，磁场 和路径方向平行，点积简化为标量乘积：

路径的长度为圆周长 ，所以积分结果为：

因此：

螺环内的总电流为：

将 代入安培环路定律：

解得螺环内部磁场大小：

可以进一步写为：

其中 是单位长度的线圈密度。