一、动量矩

1、质点的动量矩

(1) 对点的动量矩

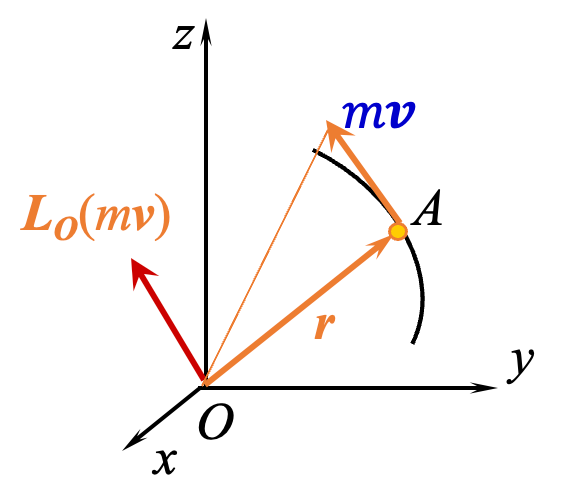
质点的动量对点的矩，定义为质点对点的动量矩：

(2) 对轴的动量矩

动量对各坐标轴的矩的解析表达式为：

比较对点的动量矩的表达式，可以得到，质点对点的动量矩在坐标轴上的投影等于质点对相应轴的动量矩。

2、质点系的动量矩

(1) 对点的动量矩

质点系内各质点对某点的动量矩的矢量和，称为这质点系对该点的动量主矩或动量矩，用表示，有：

(3) 对轴的动量矩

类似的，可以得到质点系对各坐标轴的动量矩表达式：

3、常见刚体运动的动量矩

(1) 平动刚体对固定点的动量矩

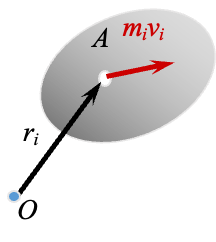
设刚体平移，刚体内任一点的矢径是，该点的质量为，速度大小为。该质点对点的动量矩为：

从而整个刚体对点的动量矩为：

因为刚体平移，则：

再一步化简，由得到：

(2) 定轴转动刚体对其转轴的动量矩

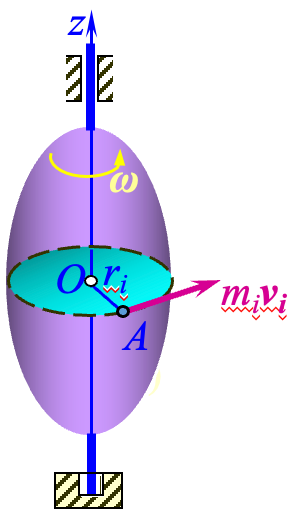
设刚体以角速度绕固定轴转动，刚体内任意一点的转动半径为，速度为，方向同时垂直于轴和转动半径，并且指向转动前进的一方。若用表示该质点的质量，则其动量对转轴的动量矩为：

从而整个刚体对轴的动量矩为：

集中为刚体对轴的转动惯量。

(3) 平面运动刚体对固定点的动量矩

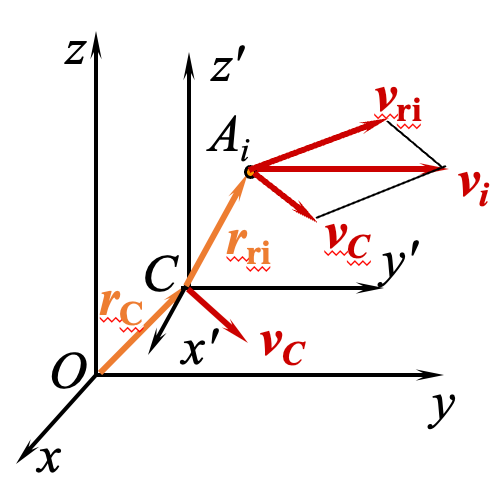
这也是质点系对固定点的动量矩的另一种表示，过固定点建立固定坐标系，以质点系的质心为原点，取平移坐标系，质点系对固定点的动量矩为：

其中，指的是质点系相对于质心的动量矩。

证明：

过固定点建立固定坐标系，以质点系的质心为原点，取平动坐标系 ,它以质心的速度 运动。设质点系内任一质点在这平移坐标系中的相对速度是，该点的绝对速度，则质点系对固定点的动量矩为：

上式的第一项化简为：

第二项化简为：

第三项化简为：

综上得到结论。

二、动量矩定理

1、动量矩定理

(1) 对固定点的动量矩定理

因为质点系对定点的动量矩为：

将其两端求时间的导数，得到：

其中可以分为外力对点的矩和内力对点的矩两项，即：

而内力对点的矩为，所以得到：

令，则：

质点系对某固定点的动量矩随时间的变化率，等于作用于质点系的全部外力对同一点的矩的矢量和（外力对点的主矩），这就是质点系对定点的动量矩定理。

(2) 对定轴的动量矩定理

将上式投影到固定坐标轴系上，注意到导数的投影等于投影的导数，则得：

质点系对某固定轴的动量矩随时间的变化率，等于作用于质点系的全部外力对同一轴的矩的代数和，这就是质点系对定轴的动量矩定理。

2、动量矩守恒定理

如果作用于质点系的所有外力对某固定点（或固定轴）的主矩始终等于零，则质点系对该点（或该轴）的动量矩保持不变。这就是质点系的动量矩守恒定理，它说明了质点系动量矩守恒的条件。

三、刚体定轴转动微分方程

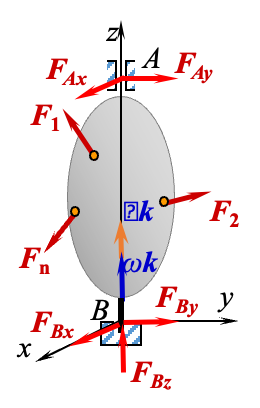
设刚体在主动力作用下绕定轴转动，与此同时，轴承上产生了约束力。用表示作用在刚体上的外力对转轴的主矩（约束力自动消去）。刚体对转轴的动量矩：

于是根据动量矩定理：

可得：

考虑到：

所以上式可以写为：

或：

这就是定轴转动的微分方程。即，定轴转动刚体对转轴的转动惯量与角加速度的乘积，等于作用于刚体的外力对转轴的主矩，这就是刚体定轴转动微分方程。

四、相对于质心的动量矩定理

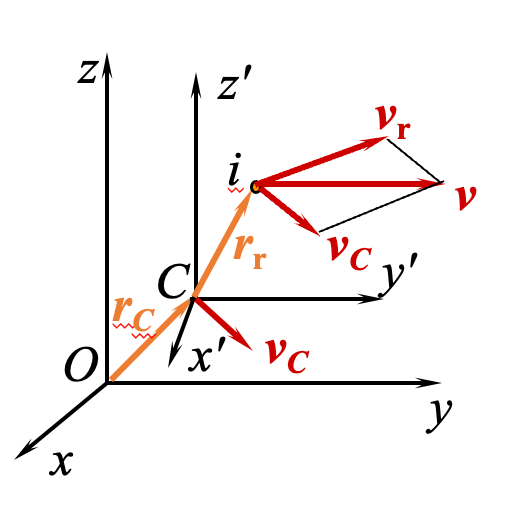
过固定点建立固定直角坐标系，以质点系的质心为原点，取平移坐标系，质点系对固定点的动量矩为：

其中即为质点系相对质心的动量矩。

1、相对于质心的动量矩定理

由对定点的动量矩定理：

有：

左边可以进行如下化简：

右边可以进行如下化简：

于是可以将方程化简为：

由质心运动定理：

所以上式可以化简为：

这就是相对于质心的动量矩定理的一般形式。即，质点系相对于质心的动量矩对时间的导数，等于作用于质点系的外力对质心的主矩。

2、相对于质心轴的动量矩定理

将前面所得质点系相对于质心的动量矩定理，沿着质心轴进行投影，得到：

这就是相对于质心轴的动量矩定理，即，质点系相对于质心轴的动量矩对时间的导数，等于作用于质点系的外力对该轴的主矩。

五、刚体的平面运动微分方程

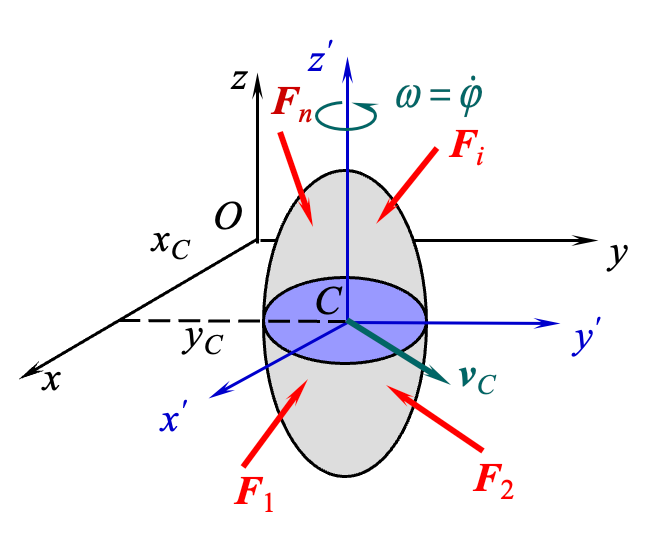
设刚体在外力作用下作平面运动。取固定坐标系，使刚体平行于坐标面运动，且质心在这个平面内，再以质心为原点作平移坐标系。

由运动学知，刚体的平面运动可分解成随基点（质心）的牵连平移和相对于基点（质心）的相对转动。随质心的牵连平移规律可由质心运动定理来确定：

而相对于质心的相对转动规律可由相对质心的动量矩定理来确定：

将前一式投影到轴上，后一式投影到上，可得：

将上面三个式子进行变形，得到：