一、反三角函数定义
1、反正弦函数
由于正弦函数的单调区间为
由于符号的习惯,我们通常用
限定在
限定在
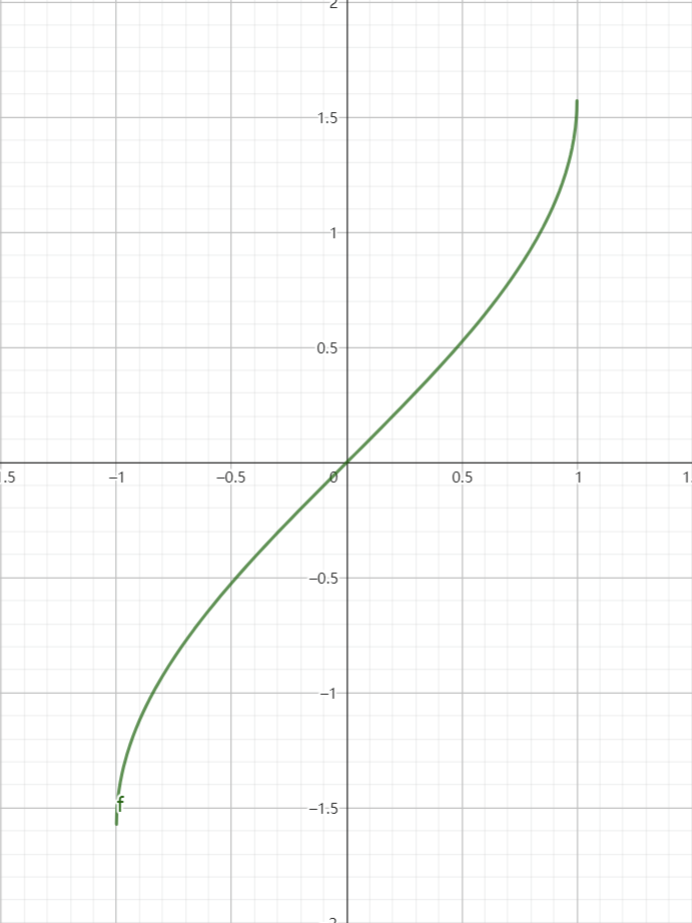
2、反余弦函数
由于余弦函数的单调区间为
限定在区间
由于符号的习惯,我们通常用
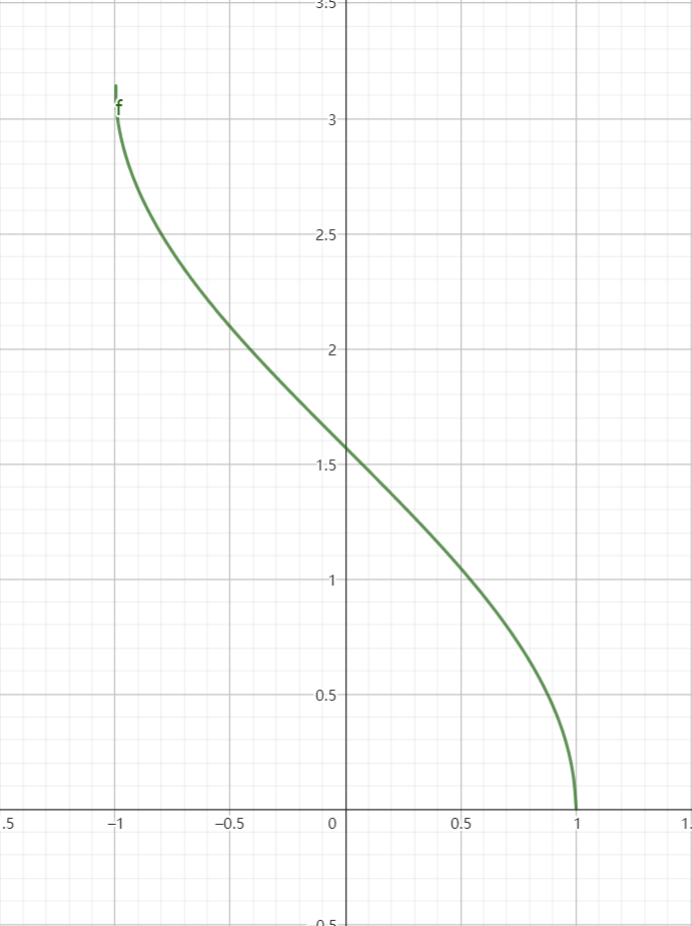
3、反正切函数
由于正切函数的单调区间为
限定在区间
由于符号的习惯,我们通常用
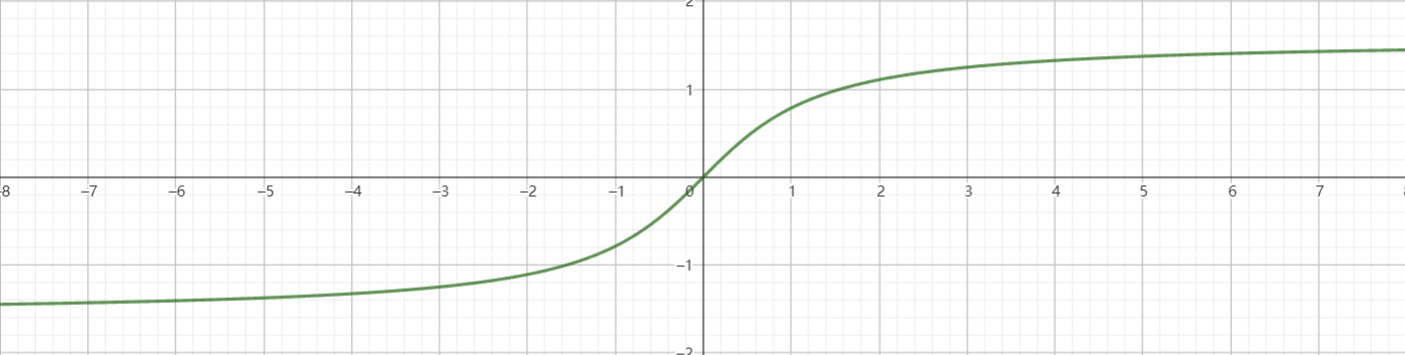
二、反三角函数的计算
例1 例1 求函数
解 定义域为
例2 求
解 设
例3 设
解 令
关注含
由于正弦函数的单调区间为
由于符号的习惯,我们通常用
限定在
限定在

由于余弦函数的单调区间为
限定在区间
由于符号的习惯,我们通常用

由于正切函数的单调区间为
限定在区间
由于符号的习惯,我们通常用

例1 例1 求函数
解 定义域为
例2 求
解 设
例3 设
解 令
关注含