模拟退火 - 老官童鞋gogo的博客

〇、爬山算法（Hill Climbing）

在介绍模拟退火之前，先简单介绍一下爬山算法。

爬山算法（Hill Climbing, HC）是一种简单直接的优化方法。它的核心思想是：从一个初始解出发，不断寻找更好的解。如果找不到更好的解，就停止。对于最小化问题，我们可以把目标函数记为，算法的基本流程如下：

在当前解的邻域中寻找一个更优解。
如果找到更优解，就移动到这个解。
如果找不到更优解，就停止（说明已经达到局部最优）。

公式表示如下：

如 果 找 到 更 优 解 否 则

爬山算法的一个问题是，它很容易卡在局部最优解上，无法找到全局最优解。比如：

局部极小值：算法停在一个“低谷”，但不是全局最低点。
平台：周围的解都一样好，算法不知道该往哪走。
脊：最优方向和允许的移动方向不一致，导致算法进展缓慢。

多嘴一句：对于连续优化问题，还可以使用梯度下降法（最速下降法）：

爬山算法的局限性在于它无法跳出局部最优解，而模拟退火通过引入“温度”参数，可以在一定概率下接受较差的解，从而跳出局部最优。

一、模拟退火

1、模拟退火的背景

模拟退火（Simulated Annealing, SA）来源于物理学中的退火过程。在高温下，原子可以自由移动，容易跨越能量障碍；随着温度降低，系统逐渐稳定到低能量状态。模拟退火将这一过程应用到优化问题中：

把目标函数看作“能量”。
把解空间看作“状态”。
用“温度”控制接受较差解的概率。

在物理学中，系统的平衡状态服从 Boltzmann 分布：

状 态

模拟退火的核心思想是通过逐步降低温度，让系统从随机状态逐渐收敛到最优解。

2、接受准则

模拟退火的关键是如何决定是否接受一个新解。我们希望构造一个马尔可夫链，使其平稳分布满足：

接受准则可以写成：

这意味着：

如果新解更优（），一定接受。
如果新解更差，以一定概率接受，概率为，其中：
- 是新解的能量与当前解的能量之差。
- 是当前温度，控制接受概率的大小。

当温度较高时，接近于，较差解更容易被接受；而当温度较低时，接近于，较差解更难被接受。

3、冷却策略

模拟退火的冷却策略决定了温度如何下降。常见的冷却方法包括：

几何降温：
指数降温：
自适应降温：根据接受率动态调整温度。

理论上，温度下降得足够慢可以保证找到全局最优解，但实际应用中需要在计算开销和精度之间权衡。

4、模拟退火的流程

伪代码：

初始化：随机生成初始解，设定初始温度。
计算当前解的能量，记录当前最优解。
当温度大于最小值时：
1. 重复若干次：
  1. 生成一个新解。
  2. 计算能量差。
  3. 根据接受准则决定是否接受新解。
  4. 更新当前最优解。
2. 降低温度。
输出最优解。

5、参数选择

初始温度：让初期接受较差解的概率较高（如 60%-90%）。
终止温度：当温度低到无法跳出局部最优时停止。
内循环次数：与问题规模成比例。
降温速率：通常在 0.85 到 0.95 之间。

二、模拟退火例题

1、题目描述

洛谷 P1337 [JSOI2004] 平衡点 / 吊打XXX

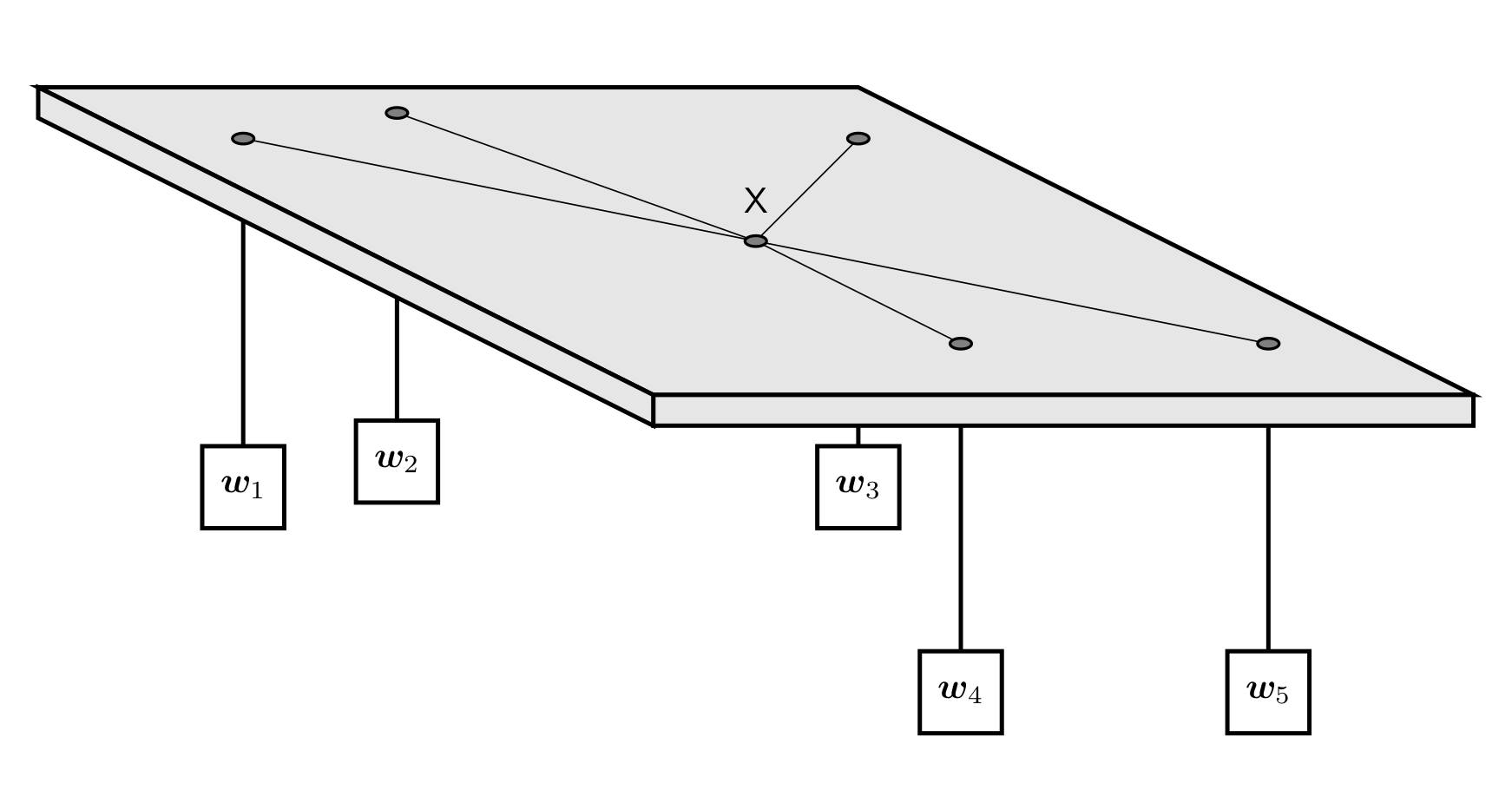
如图，有个重物，每个重物系在一条足够长的绳子上。

每条绳子自上而下穿过桌面上的洞，然后系在一起。图中处就是公共的绳结。假设绳子是完全弹性的（即不会造成能量损失），桌子足够高（重物不会垂到地上），且忽略所有的摩擦，求绳结最终平衡于何处。

注意：桌面上的洞都比绳结小得多，所以即使某个重物特别重，绳结也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。

输入格式

文件的第一行为一个正整数（），表示重物和洞的数目。

接下来的行，每行是个整数，分别表示第个洞的坐标以及第个重物的重量。（）

输出格式

你的程序必须输出两个浮点数（保留小数点后三位），分别表示处于最终平衡状态时绳结的横坐标和纵坐标。两个数以一个空格隔开。

2、题目分析

关于这道题，一切自然变化进行的方向都是使能量降低，因为能量较低的状态比较稳定。因为物重一定，桌子下面绳子越短，重物越低，势能越小，反过来，桌面上的绳子越长，重物越高，势能越大。

设第个洞的位置为，重物重量为，绳结的位置为。根据势能的计算公式：

以桌面作为零势能面，桌面以上为正方向，其中表示第个重物的势能，是重物的质量，是重力加速度，是重物的高度。而重物的高度可以表示为，（是绳子的原始长度，是桌面上的绳子长度）

最后，势能的总和即为：

推导结果的前一项为定值，所以只需要后一项的值最小。因此要求的平衡点就是使下方函数取到全局最小值的点。

然后就可以使用模拟退火算法来求解这个函数的全局最小值，具体实现方法查看后面的内容。

3、代码拆解

（1）数据读入以及初始选点

1
scanf("%d", &n);
2
for (int a = 1; a <= n; a++) {
3
    scanf("%d%d%d", &object[a].x, &object[a].y, &object[a].w);
4
    ansx += object[a].x;
5
    ansy += object[a].y;
6
}
7
ansx /= n;
8
ansy /= n;
9
answ = energy(ansx, ansy);

首先读入数据，并将所有洞的坐标取平均作为初始点，当然初始点位可以是任意位置。

（2）能量计算函数

1
double energy(double x, double y) {
2
    double r = 0, dx, dy;
3
    for (int a = 1; a <= n; a++) {
4
        dx = x - object[a].x;
5
        dy = y - object[a].y;
6
        r += sqrt(dx * dx + dy * dy) * object[a].w;
7
    }
8
    return r;
9
}

这个函数计算当前点的能量值，即所有重物的势能之和。

（3）模拟退火主循环

1
void sa() {
2
    double t = 3000;
3
    while (t > 1e-15) {
4
        double nx = ansx + (rand() * 2 - RAND_MAX) * t;
5
        double ny = ansy + (rand() * 2 - RAND_MAX) * t;
6
        double nw = energy(nx, ny);
7
        double de = nw - answ;
8
        if (de < 0) {
9
            ansx = nx;
10
            ansy = ny;
11
            answ = nw;
12
        } else if (exp(-de / t) * RAND_MAX > rand()) {
13
            ansx = nx;
14
            ansy = ny;
15
        }
16
        t *= down;
17
    }
18
}

这是模拟退火的核心部分，首先初始设置一个比较高的温度，然后在温度大于一个很小的值时不断循环。在每次循环中，生成一个新的候选点，计算其能量值，并根据能量差决定是否接受这个新点。如果新点能量更低，则一定接受；如果能量更高，则以一定概率接受（概率的设置回见上文，此处 exp(-de / t) * RAND_MAX > rand() 就是概率的代码表示方法）。最后逐步降低温度。

当然，模拟退火算法是一个看脸的算法，为了提高结果的稳定性，可以多次运行模拟退火算法，取最优结果。

4、完整代码

1
#include <bits/stdc++.h>
2

3
using namespace std;
4
int n;
5
double down = 0.996;
6
struct node {
7
    int x;
8
    int y;
9
    int w;
10
}
11
object[2005];
12
double ansx, ansy, answ;
13
double energy(double x, double y) {
14
    double r = 0, dx, dy;
15
    for (int a = 1; a <= n; a++) {
16
        dx = x - object[a].x;
17
        dy = y - object[a].y;
18
        r += sqrt(dx * dx + dy * dy) * object[a].w;
19
    }
20
    return r;
21
}
22
void sa() {
23
    double t = 3000;
24
    while (t > 1e-15) {
25
        double nx = ansx + (rand() * 2 - RAND_MAX) * t;
26
        double ny = ansy + (rand() * 2 - RAND_MAX) * t;
27
        double nw = energy(nx, ny);
28
        double de = nw - answ;
29
        if (de < 0) {
30
            ansx = nx;
31
            ansy = ny;
32
            answ = nw;
33
        } else if (exp(-de / t) * RAND_MAX > rand()) {
34
            ansx = nx;
35
            ansy = ny;
36
        }
37
        t *= down;
38
    }
39
}
40
int main() {
41
    scanf("%d", &n);
42
    for (int a = 1; a <= n; a++) {
43
        scanf("%d%d%d", &object[a].x, &object[a].y, &object[a].w);
44
        ansx += object[a].x;
45
        ansy += object[a].y;
46
    }
47
    ansx /= n;
48
    ansy /= n;
49
    answ = energy(ansx, ansy);
50
    for (int i = 1; i <= 5; i++)
51
        sa();
52
    printf("%.3lf %.3lf\n", ansx, ansy);
53
    return 0;
54
}

老官童鞋gogo