1. 转轴通过圆环中心与环面垂直的转动惯量

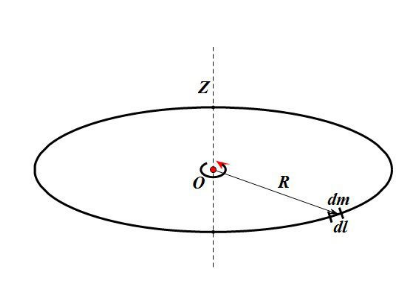
推导：
在圆环上取一质元，其质量为 ，其中 为线密度， 为圆弧元。质元对转轴的元转动惯量为：

对整个圆环积分：

代入 ，得：

2. 转轴沿圆环直径的转动惯量

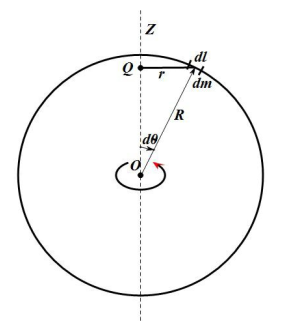
推导：
质元质量 （ 为质元与转轴的夹角）。质元的转动惯量元为：

利用三角恒等式 ，积分得：

第二项积分 ，故：

3. 转轴通过薄圆盘中心与圆盘垂直的转动惯量

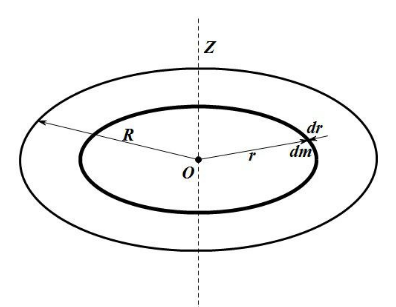
推导：
取半径为 、宽度 的细圆环，质量 （面密度 ）。转动惯量元为：

积分得：

代入 ，得：

4. 转轴沿圆筒几何轴的转动惯量

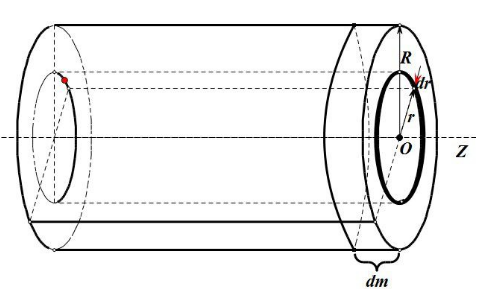
推导：
将圆筒视为由无数同心圆环组成。取半径 的元圆筒，质量 ，转动惯量元为：

总转动惯量为内外半径积分之差：

因 ，代入得：

5. 转轴沿圆柱体几何轴的转动惯量

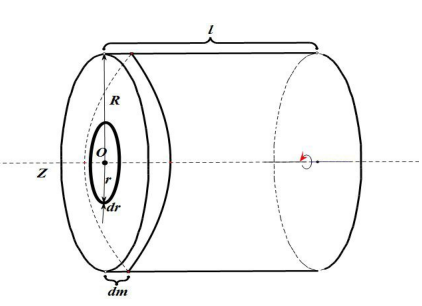
推导：
将圆柱体分解为无数薄圆盘。取厚度为 的微圆盘，质量 （ 为体密度）。薄圆盘的转动惯量元为：

总转动惯量为：

因总质量 ，代入得：

6. 转轴通过圆柱体中心与几何轴垂直的转动惯量

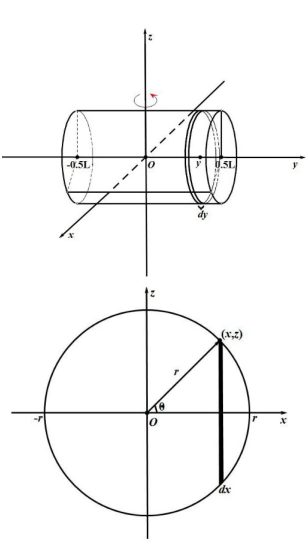
推导：
取微细长方体，坐标 ，质量元 （）。转动惯量元为：

转换为极坐标：，积分得：

分离积分并计算，最终结果为：

7. 转轴通过细棒中心与棒垂直的转动惯量

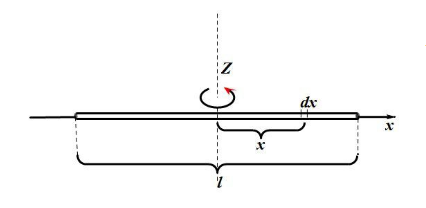
推导：
取质元 （线密度 ），距转轴距离为 。转动惯量元为：

积分区间为 到 ：

代入 ，得：

8. 转轴通过细棒端点与棒垂直的转动惯量

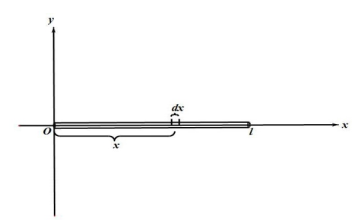
推导：
积分区间改为 到 ，转动惯量元相同：

代入 ，得：

9. 转轴通过球体沿直径的转动惯量

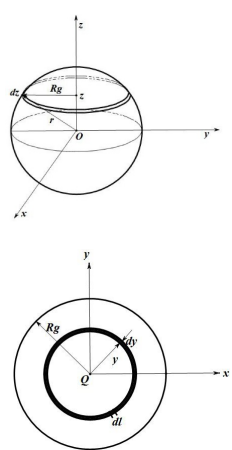
推导：
将球体分解为薄圆盘。取距球心 处厚度 的圆盘，半径 ，质量 。圆盘转动惯量元为：

总转动惯量为：

展开积分并计算，结合总质量 ，得：

10. 转轴沿球壳直径的转动惯量

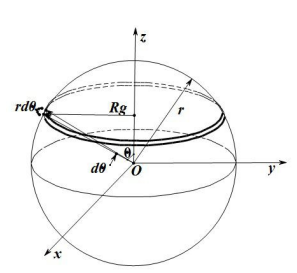
推导：
取圆心角 的圆环，半径 ，质量元 （面密度 ）。转动惯量元为：

积分得：

代入 ，得：

11. 转轴沿底面是正方形的长方体的几何轴的转动惯量

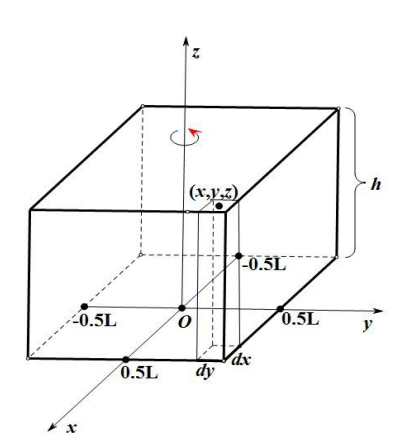
推导：
取微元 ，转动半径 。转动惯量元为：

在 区域积分：

代入总质量 ，得：

12. 转轴沿圆盘直径的转动惯量

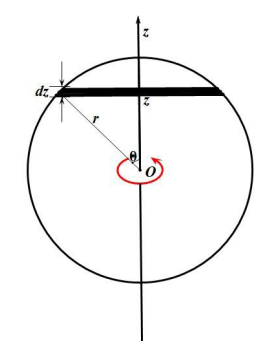
推导：
取宽度 的长条，长度 ，质量元 。转动惯量元为：

总转动惯量：

代入 ，得：