一、复数的定义及各种表达形式

1、代数定义

1. 如果量能写成如下形式： 则称 是一个复数。这里是一个符号，称作虚数单位。实数分别称作复数的实数部分（或简称实部）和虚数部分（或简称虚部），记为：

2. 复数的全体所组成的集合记为

3. 实数是虚部为零的复数。 当时，复数简记为.此时，称 复数为纯虚数 当时，复数简记为. 当时，复数简记为. 简记实部和虚部均为零的复数为.

4. 依据约定，我们有 . 对于任意的两个复数,当且仅当且时，我们称与相等，记为.

5. 依据约定，我们有：

2、几何意义

取平面上的一点作为参照点并记为,过点作相互垂直的两条实数轴，两条数轴都以作为原点， 并具有相同的单位长度。习惯上，我们总是让其中的一条数轴的正向向右，另一条数轴的正向朝上，即构建了一个平面笛卡尔坐标系。

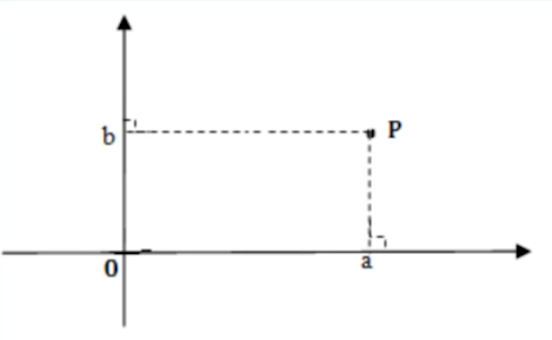
已知复数,这里，如图构造，在平面上的唯一对应点，这里点在由点及横竖两数轴所构成的平面坐标系中的坐标为.

反之，若已知平面上的点，它在在由及横竖两数轴所构成的平面坐标系中的坐标为，则存在唯一的复数满足.据此，我们不难获知，复数与上述平面上的点——对应。习惯上，我们称这样的平面为复（数）平面。称水平数轴为实轴，称竖向数轴为虚轴，记为. 我们常将复平面上与给定复数对应的点直接标注为 由于平面坐标系中的点与向径是一一对应的，因此，复平面上的复数也就与向径（有向线段）一一对应。

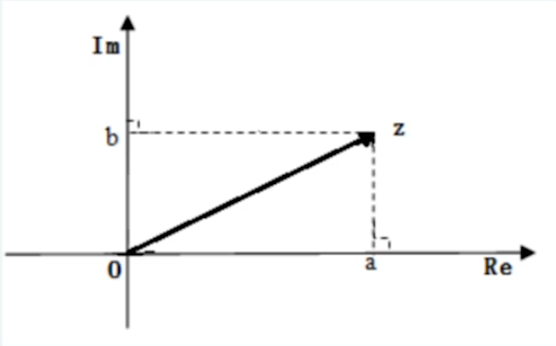
以后，复数、复平面上与之对应的点及向径为同一体，不做区分。

3、三角函数表达形式

1. 已知复数,这里 的模长：有向线段 的长度，记作.

2. 的幅角：称复平面上的有向线段与实轴正向的夹角为的辐角。

约定： ：当实轴的正方向向量按逆时针旋转角度到有向线段 时。 ：当顺时针旋转角度到有向线段时。

3. 的三角函数形式：

二、共轭复数

已知复数，这里.我们称如下定义的复数： 为复数z的共轭复数。

在复平面上，复数与共轭复数关于实轴对称。

存在运算规律：

三、复数的运算规律

1. 对于任意复数，都有：,

2. 复数的乘法运算是指任意两个复数的求积过程。两个复数的积如下定义并记号： 对于给定的两个复数 这里. 复数与的积是一个记为 的新复数： 如同实数运算那样，我们也记

   依据复数的乘法公式，可得如下重要等式： 事实上， 往往被看成为之所以引入虚数单位的原因：为了解决 的求解问题 我们也记：

[card title=“为什么要以这种方式学习复数” color=“info”]借助于复数的形式表达，通过定义乘法运算，最后推得，而恰恰是高中数学中学习复数的出发点，也是历史上讨论复数的出发点。而此时不通过这里开始讨论复数，虽然这样比较直观，但是这样存在一个逻辑性上的小问题，是复数与复数的乘法，但是我们这个时候并没有复数的定义及其乘法运算。两种出发点，一个比较直观，是数学的来源，一个是依据数学本身的逻辑关系来产生的一套理论，这两个之间就存在着直观和抽象的相对关系。[/card]

3. 对于任意复数，都有：,

4. 复数的消去律：对于任意复数，若，则或者.

例1 证明复数的消去律。

**证明：**对于任意复数，若 ,则： 由于均为实数，依实数乘法运算的消去律，我们有或. 当时，依复数模长的计算公式，我们有，故 . 同理可证，当时，. 综上所述，我们有 或.

5. 若 ，，这里 ，且 ，则不难知：
6. 复数的三角不等式：对于任意复数 ，.

四、复数乘除法的几何意义

对于任意复数,不妨设：

这里 分别是复数 的辐角。则依复数加法及乘法运算的规律，我们有：

也就是说，两个复数相乘，在复平面上就是两个复数的模长相乘，辐角相加。

同样地，复数除法的几何意义是在复平面内，商的模等于被除数和除数的模的商，商的辐角等于被除数和除数的辐角的差。

五、复数的欧拉（Euler）公式

复数的欧拉公式表达式为：

若复数，则：

在欧拉公式中，令 并移项，则：

六、复数的棣莫弗（De Moivre）公式

复数的棣莫弗公式表达式为：

例2 证明棣莫弗公式

**证明：**对，采用数学归纳法证明。 当时，等式明显成立。 设当时等式成立，则当时： 即当时等式也成立。 综上，对于任意正整数，都有

借助欧拉公式，我们可以非常容易地证明上述公式。

例3 用欧拉公式证明棣莫弗公式

**证明：**把所有的复数改写成指数的形式，即 则

使用欧拉公式展开可以得到棣莫弗公式。

若复数，则：