引言

数学粗略地说是由三个大的分支组成：几何学、代数学和分析学。他们都离不开数这个基本概念。例如从“微积分”开始的分析学，是建立在严格的极限理论基础上的，而这一理论所依赖的就是实数体系的连续性。因此，要学好数学，必须先学习数的理论。

一、素数

1、素数的定义与检验

素数在数中占有异乎寻常的地位，素数的理论初步建立在欧几里得的《几何原本》之中。定义为一个大于的自然数，如果除了和其自身外，不能被其他自然数整除，则称此自然数为素数（质数），否则称为合数。例如：都是素数。

【注】和既不是素数，也不是合数。

检验素数的基本方法：用到 之间的所有整数去除，均无法整除，则为素数。

2、素数的性质

定义：若只有1能同时整除自然数与，即不存在大于的自然数同时整除与, 则称与为互素的（或互质的）。

定理1： 互素的两个自然数是与它们有同比自然数对中最小的。即：设为自然数，如果,且互素，则.

定理2：（欧几里得引理）若素数整除两自然数之积(记为 ),则（整除）或（整除）.

定理3：（裴蜀定理）若是整数，且它们的最大公约数，那么对于任意的整数和，整数必是的倍数。特别地，一定存在整数，使成立。 推论：互素的充分必要条件是存在整数使

**例1：**求平面上整点(两个坐标皆为整数的点)到直线的距离的最小值。

**解：**由点到直线的距离公式知整点到的距离为，而由裴蜀定理知为的倍数，所以当 时，取最小值：

定理4：（算术基本定理）任何一个大于的自然数，如果不是素数，那么可以唯一分解为有限个素数的乘积： ，其中为素数，指数为正整数。例如，，等等。

**定理5：**素数有无穷多个。

证明：用反证法。假设素数只有有限多个，设为个：. 记，有. 那么： 若为素数，则与“素数只有个”矛盾； 若为合数 , 则可分解为若干个比它小的素数之积，而不可能被 整 除，所以还存在不同于的素数，这又与“素数只有个”这个假设矛盾。 综上可得，素数有无穷多个。

3、孪生素数和哥德巴赫猜想

相差的两个素数称为孪生素数。例如：和，和，和，和等等。“存在无穷多对孪生素数”这就是著名的孪生素数猜想，至今未得到证明，但数学家们相信这是正确的。

数论是数学的一个重要分支，主要研究整数性质以及和它有关的规律与理论。数论研究中最著名的猜想应该是“哥德巴赫猜想”了。1742年，哥德巴赫给欧拉的信中提出了：“任一大于的偶数都可表示成两个素数之和。“这就是著名的哥德巴赫猜想，我们常常简称为“1+1”。

三、有理数和无理数

1、有理数的性质

1. 有理数四则运算的封闭性：有理数与有理数进行加减乘除运算后还是有理数。

2. 有理数的稠密性：任意两个不同的有理数之间存在无数个有理数。

3. 有理数的可公度性：所谓可公度量，亦称为可通约量，是数学的基本概念之一，指两个同是第三个量的整数倍的量.对于两个量与,若存在第三个量, 使同时成立，这里为自然数，则称量与量可公度或可通约，且称是A与 的一个公度，这时称与 是可公度量或可通约量.若不存在自然数 与量,使 成立，则称与 是不可公度或不可通约，这时是不可公度量或不可通约量。

   任意两个有理数和存在公倍数，即，设，那么有

   （可公度性的集合意义）辗转相截：两条线段长度为有理数，用 去截，若剩下，则用去截，若剩下。则用去截必可经有限次相截刚好截完。

   设,则

   其中为的一个公度。

2、无理数的性质

1. 正方形的边长与其对角线长不可公度： 如图，设正方形边长为，将边长与对角线辗转相截：在上截得，过点作的垂直平分线。有，于是，接下来即为小正方形的边长去截其对角线，这样可以无穷无尽地截下去，永远截不完…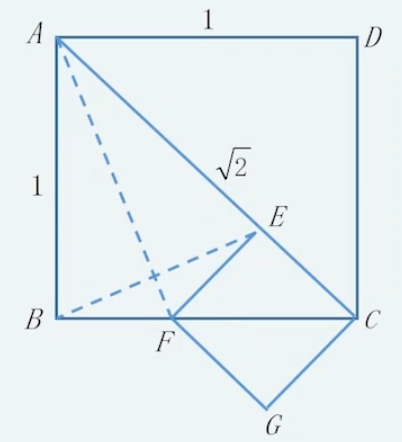

   

2. **定义：**不能表示成两个整数之比的数称为无理数。

   ---

   例2：是无理数 证明：（反证法）假设（为互素的正整数），那么有，所以是偶数，记是偶数，与互素矛盾。因此是无理数。

   ---

   **例3：**证明：如果不是完全平方数（等于某整数的平方的正整数），则为无理数。 证明：（反证法）假设，那么. 因为不是完全平方数，所以不是整数，存在使得，即. 考察 ，于是有.其中.也就是说可找到正整数 ,使得假设那么用代替可进行以上“操作”，又可以找到正整数，使得假设 这样的“操作”可以一 直进行下去，这是不可能的，因为是有限的自然数。矛盾。 从以上例子可以看到，无理数有无穷多个。

   ---

​ 其实，无理数远不止这些.有理数与无理数统称为实数，实数布满了整个数轴。

四、代数数与超越数（实数范围内）

1. 代数数定义：如果是某整系数多项式（其中为正整数，,为整数，）的根，则称为代数数。

​ 例如： ​ (1)任意有理数为代数数，因为它是一次整系数多项式 的根。 ​ (2)是代数数，因为它是二次整系数多项式的根。

2. 代数数经加、减、乘、除（分母不为零）四则运算后仍为代数数。

3. 不是代数数的数称为超越数，例如是超越数。

4. 可以证明，当为有理数时，是代数数，而 是超越数。

五、等势集与可列集

1. 定义：设为两个集合，如果存在一个从到的一一对应映射(双射)，则称集合与集合等势，也称与是等势集。记作.

2. 两个有限集合等势当且仅当两个集合的元素个数相等。

3. 空集只与空集自身等势。

4. 等势具有如下性质：

   (1)自反性：. (2)对称性：若,则. (3)传递性：若,则.

例如： 全体正整数集和全体偶数集等势。可作双射 自然数集和全体整数集等势。可作双射

5. 定义：如果集合与自然数集等势，则称集合是可列的（或可数的）。对应之前所学：可数集。

   正整数集、整数集都是可列的，全体有理数集也是可列的。我们只要考虑全体有理数集中的元素是否可以排成一个队列，显然只要考虑正有理数的情形即可。我们以有理数（分数）的分母大小为序，写出所有正有理数如下：

   

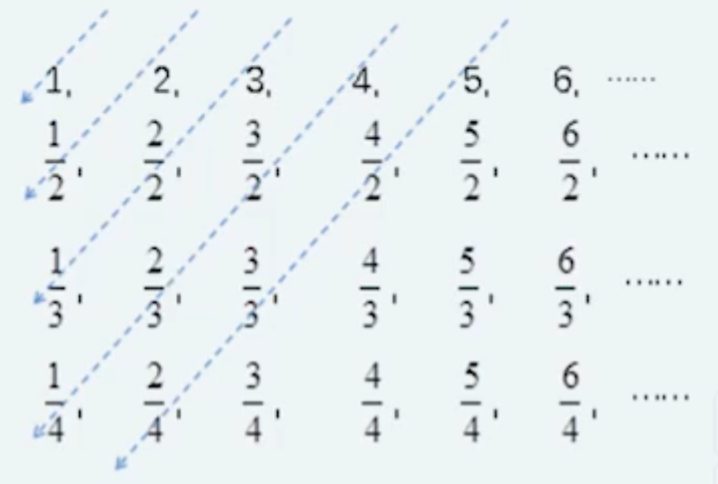
   现从左上角开始，按箭头方向将所有的数排成队列(跳过前面已出现的数字 ，

   这样就把所有的正有理数排成队列了。如果我们将排在第一位，然后将每个正有理数的相反数插入到自己的后面，那么就把全体有理数排成队列了，因此全体有理数集是可列的。

6. 上的实数与上的实数是等势的。上的实数与实数集也是等式的。

   

7. 反证法证明全体实数是不可列的（无理数是不可列的），即证上的实数是不可列的。 假设上的实数可列。 我们用小数表示，可和自然数对应如下：

   现取内一数，使得：（且）这样，数不在对应的队列中， 因为和队列中的数至少有一位数字不同。矛盾。 所以，上的实数不可列。即全体实数（无理数）是不可列的。

8. 若集合可列，那么集合是可列的。

9. 现取无理数集的一个真子集： ,显然它与有理数可一一对应，即与有理数集等势，所以说无理数此有理数多。 另外可以证明：全体代数数集是可列的，全体超越数集是不可列的。