一、静电场的环路定律

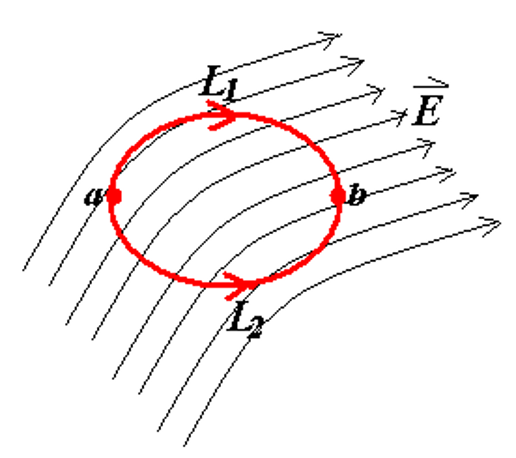
我们根据图示逐步推导静电场的环路定理（即闭合路径上的电场沿路径积分为零）。静电场是由静止电荷分布产生的。对于静电场来说，其电场 与电势（）满足关系：

电势是标量场，描述了静电场各点的能量。设路径沿 （如图中的闭合回路），则电场的环路积分可以表示为：

其中是路径上的微小位移向量。如图所示，我们考虑沿环路的积分路径，有两个部分和 ，分别从点 到点 ：

• ：路径沿电场线，从 到 。
• ：路径逆电场线，从 返回到 。

电场 是保守场，也就是说电场的环路积分仅与路径的起点和终点有关。换言之，电场的环路积分与电势差有关：

• 在路径 上，从 到 ：
• 在路径 上，从 返回到 ：

将两个路径积分相加，我们得到沿闭合路径 的环路积分：

于是：

从以上推导可以得到，静电场的环路积分恒为零：

二、电势的应用

1、在电偶极子上应用电势

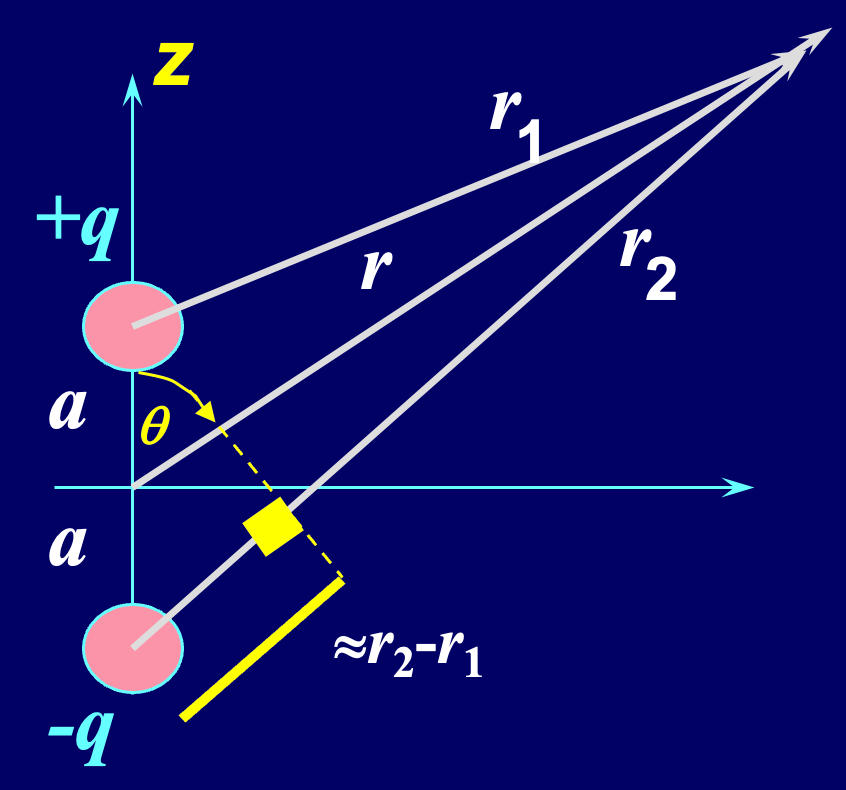
由于电势是标量，所以计算电势和的运算非常简单。首先根据公式，写出研究点的电势大小：

由于，则可以做出如下近似：

化简得：

2、在电四偶极矩上应用电势

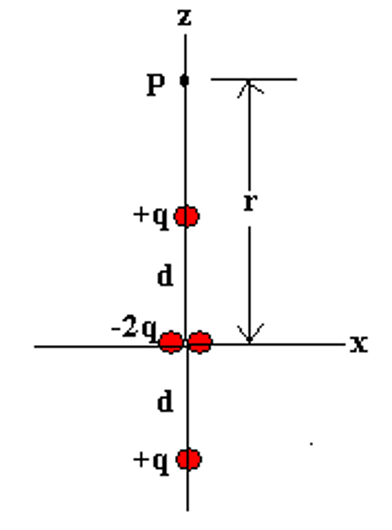
首先写出原始计算公式：

因为，则可以化简为：

其中，成为四偶极矩。

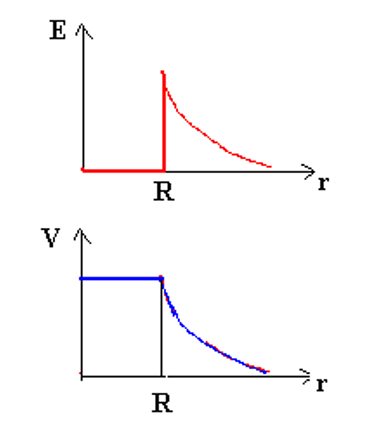
3、研究均匀带电球壳的电势

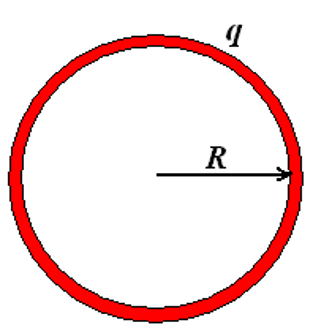
根据高斯定理：

积分，得到对应位置的电势：

1. 当时：

2. 当时：

做出对应图像：

4、研究均匀带电圆环的电势

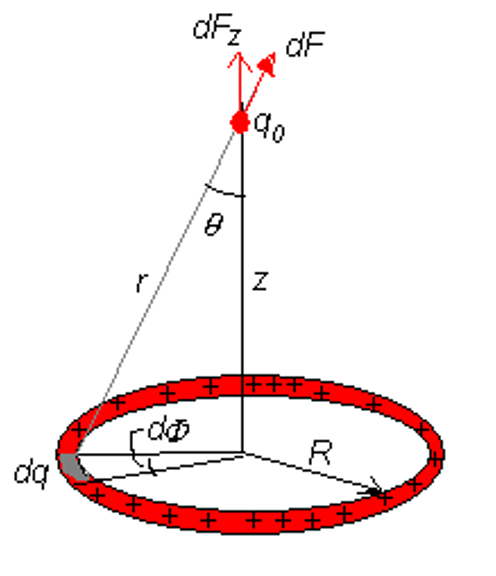
使用代数积分计算即可，首先写出对研究点产生的电势：

积分运算：

5、研究均匀带电圆盘的电势

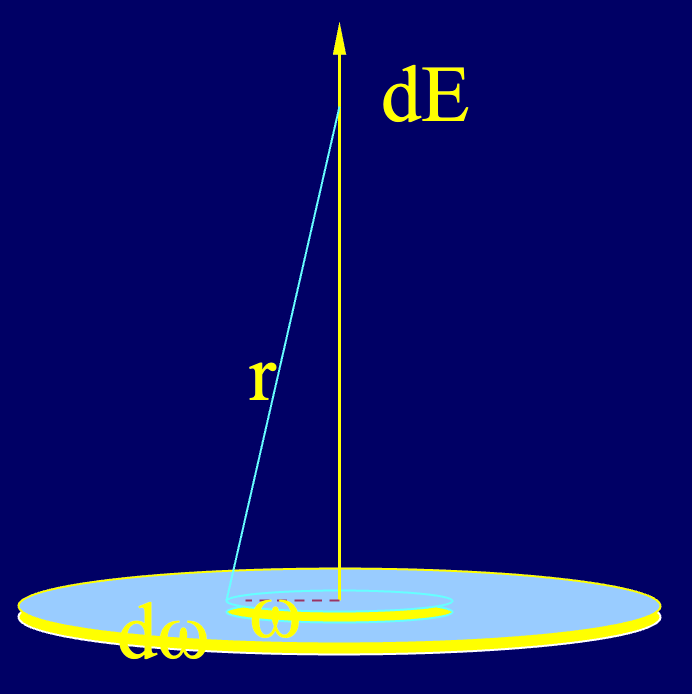
将圆环细分为无穷多个均匀带电圆环，利用应用四的方法进行积分：

然后对积分：

特别地，当时，对根号里面的内容进行变形和泰勒展开，得到：

也就是说，当距离圆盘足够远时，可以将圆盘看作是点电荷。

6、根据电势计算电场

已知空间内的电势，可以通过下面公式计算电场：

展开为：

在球坐标系中，经过变量代换得到：

例：

已知电势，可以求出电场，所以可以使用这种方法求出电偶极子在任意位置的产生的电场。

已知电势：

对进行极坐标系变换：

代入得：

注意，这里是近似之后的结果，忽略了距离带来的部分效应。比较电偶极子在特殊位置下产生的电场，可以发现二者相同（注意将近似处理，）。

同样地，上面电势的应用中所求的问题，都可以使用该方法求解出电场。

三、等势

四、尖端放电

上图是两个导体球，中间用一根导线连接，由于导体是个等势体，表面是个等势面，则两球表面的电势相等，有公式：

根据面电荷密度的计算公式：

得到：

所以（曲率）半径越小，面电荷密度越大，更容易放电。