一、初瞬时问题

初瞬时问题，即系统本来静止，突然因为某个原因导致开始运动。

例1：

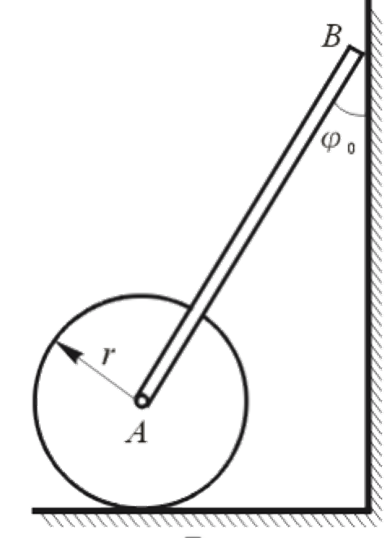
均质杆的质量为，长度为，上端靠在光滑的墙壁上，下端与圆柱的中心铰接。均质圆柱的质量为 ，半径为，可沿固定水平面滚动而不滑动。假设系统在位置由静止释放，试求在初瞬时圆柱质心的加速度。

解：

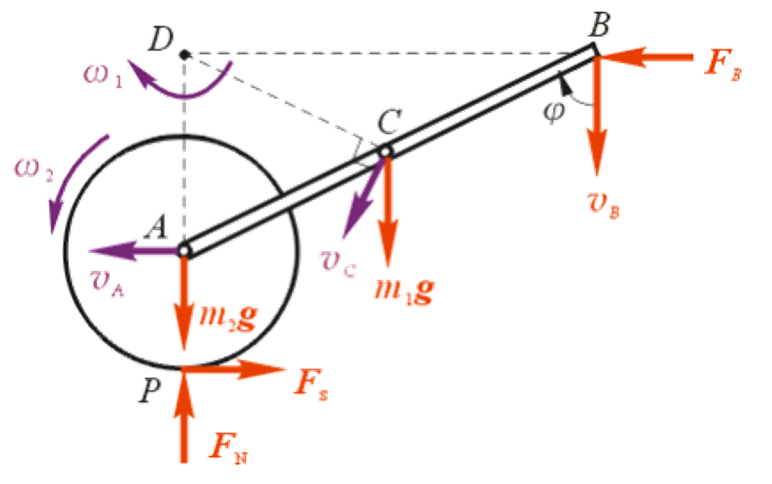
考虑从初始条件开始，到任意角度时系统的情况，代入初始条件从而求解。

应用动能定理：

由运动学知识可知：

得系统的动能为：

因为只有重力作功，故：

应用动能定理的微分形式：

同时考虑到：

得：

所以圆柱质心的加速度为：

因为在运动初瞬时：，得到：

本题也可以用平面运动微分方程求解，分别对杆和圆轮列出平面运动微分方程，并补充运动方程即可，共有七个未知量，可以列出七个方程。过程比使用动能定理繁琐。

但是，动能定理方法存在缺点，因为要使用动能定理完成题目，需要对一个运动过程列出一般形式的动能定理。

例2：

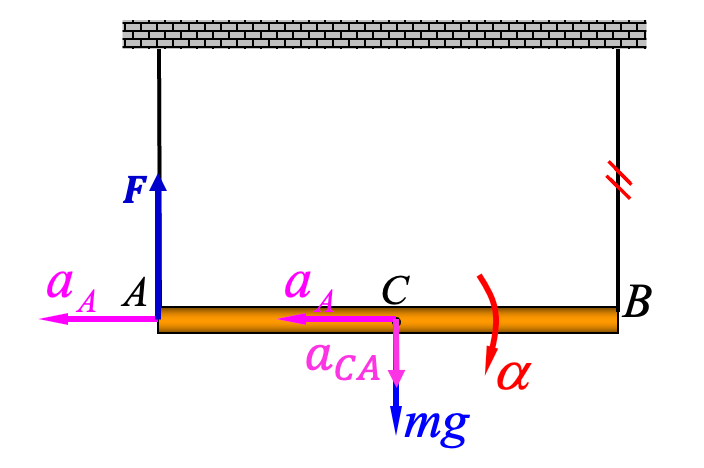
一根匀质杆长度为，绳子断开的瞬时，求解杆的转动角加速度。

解：

竖直方向上列出动量定理的微分形式：

列出相对质心的动量矩定理：

解得：

对于初瞬时问题（突然解除约束力问题），优先使用动能定理的微分形式，不能用或者是很麻烦时，改用平面运动的微分方程联立求解。

二、中间态问题

例3：

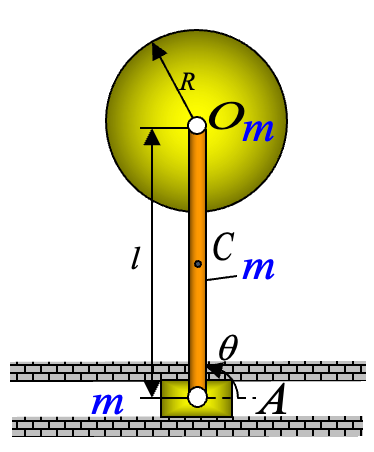
如图所示，滑块与半径为的均质轮用长为l的均质杆相铰联，滑块可在水平槽中滑动，在重力作用下，轮由图示不稳定的平衡位置静止开始运动，设三构件质量均为，不计摩擦，试求任意倾角位置时：

(1) 杆的角速度与角加速度。

(2) 滑块受到来自滑道的约束力。

解：

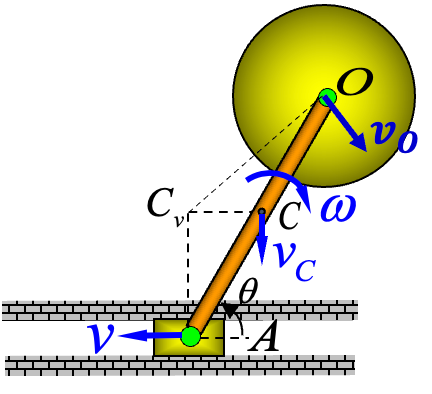
注意系统在水平方向动量守恒，系统质心恒在杆中点，水平方向动量恒为零，点速度沿铅垂方向。设杆速度瞬心为：

由，有：

解得：

由动能定理的微分形式（注意），对上面的方程两边求导，得到：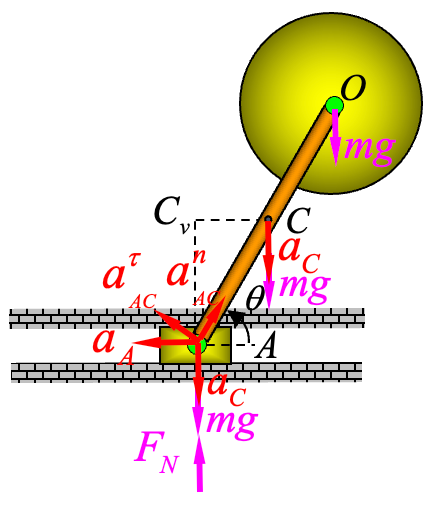

研究整体，对整体使用质心运动定律：

又由，解得：

最终：

例4：

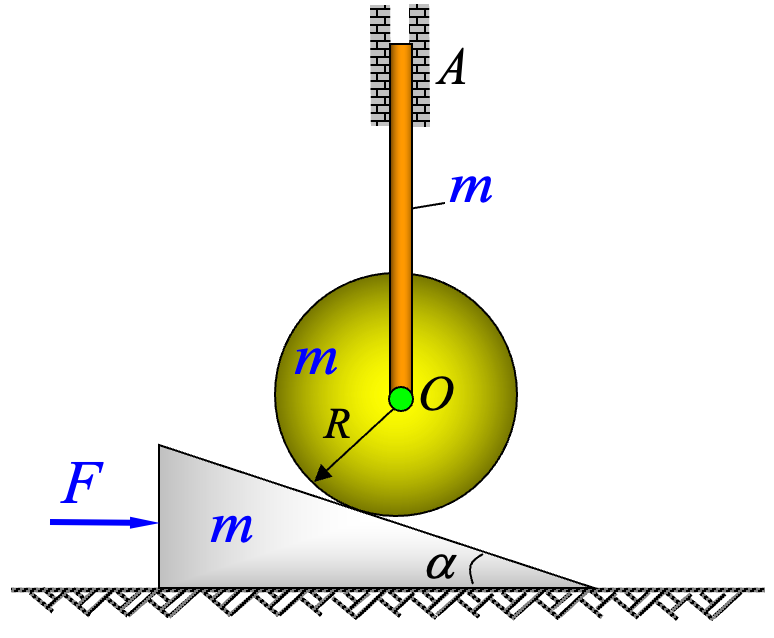
如图所示，斜面倾角为，在水平力作用下，沿水平面向右移动，并带动半径为的均质轮在斜面上纯滚动，铅直杆与轮心较接，不计摩擦，设三构件质量均为，系统初始静止，试求斜面加速度及较处反力。

解：

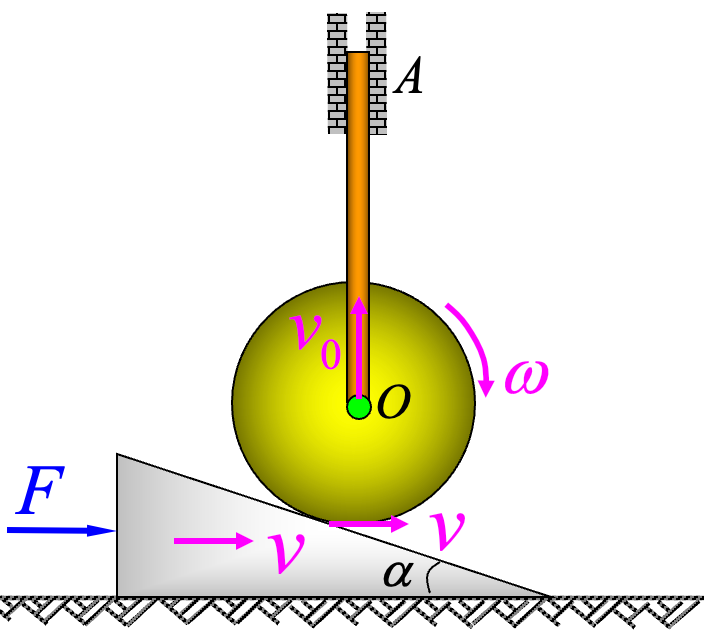
设系统从静止状态开始，斜面向右移动距离时速度为，可以写出如下计算方程：

由，且，得到：

将变量代入上式，两边对时间求导，得：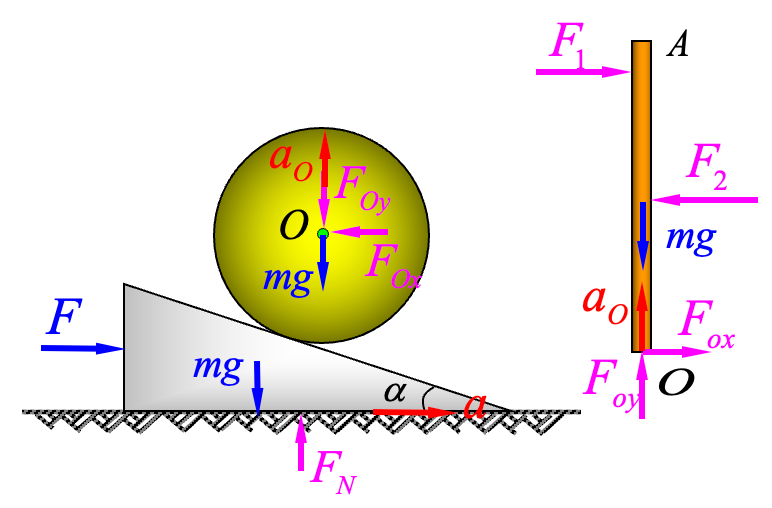

然后分别研究轮与斜面系统、杆，受力如上图，对于轮与斜面的系统，由质心运动定理：

对于杆，由质心运动定理：

对于中间态问题，宜先用动能定理求出速度和加速度，再用动量（矩）方法求解约束力。

三、末瞬时问题

例5：

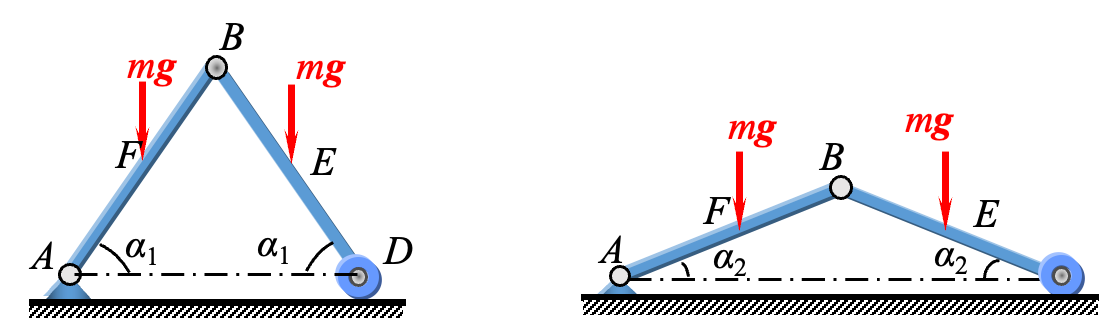
系统在铅直平面内由两根相同的匀质细直杆构成，，为铰链，为小滚轮，且水平。每根杆的质量为，长度为，当仰角时，系统由静止释放。试求当仰角减到时，杆的角速度及角加速度，摩擦和小滚轮的质量都不计。

解：

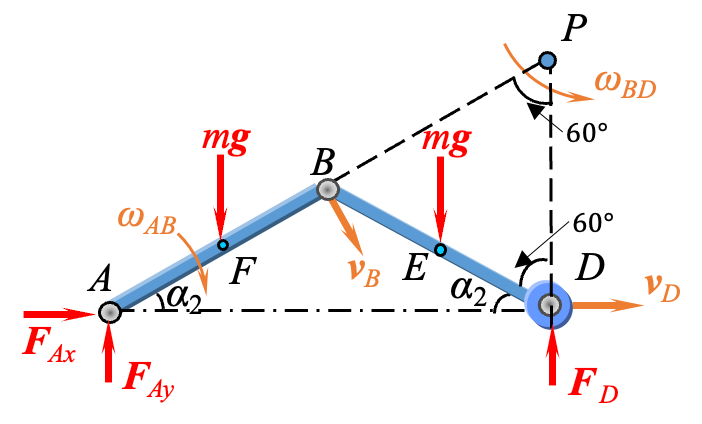
取整个系统作为研究对象，其中杆做定轴转动，做平面运动。考虑系统由静止到这个过程。系统开始时保持静止，初动能。末动能等于：

由图，杆的速度瞬心在点，分析点的速度为：

由于，地：

杆质心的速度：

而：

将上面结果代入，得到：

在运动过程中，只有杆的重力做功，于是作用在系统中的力在运动过程中的总功为：

由得：

从而得到角速度：

如果想要求角加速度，绝对不可以直接将上式特殊情况下的等式直接求导，应当利用任意角度的动能定理方程两边求导获得角加速度。