一、达朗贝尔原理

1、质点达朗贝尔原理

设质量为的非自由质点，在主动力和约束力作用下沿曲线运动，该质点的动力学基本方程为：

或：

引入质点的惯性力的概念，于是上式可以写为：

上式表明，在质点运动的每一瞬时，作用于质点的主动力、约束力和质点的惯性力在形式上构成一平衡力系。这就是质点的达朗贝尔原理。

2、质点系达朗贝尔原理

质点的达朗贝尔原理可以直接推广到质点系，将达朗贝尔原理应用于每个质点，得到个矢量平衡方程。

这表明，在质点系运动的任一瞬时，作用于每一质点上的主动力、约束力和该质点的惯性力在形式上构成一平衡力系。对于讨论的质点系，有个形式如上的平衡方程，即有个形式上的平衡力系，将其组合在一起，所构成的任意力系仍然是平衡力系，根据静力学中空间任意力系的平衡条件，有：

上式表明，在任意瞬时，作用于质点系的主动力、约束力和所有质点的惯性力在形式上构成平衡力系：力系的主矢等于零，该力系对任一点的主矩也等于零。这是质点系的达朗贝尔原理的一种表述。将主动力和约束力合起来看作是外力，则上式可以写为：

上式表明，在任意瞬时，作用于质点系的所有外力和所有质点的惯性力在形式上构成平衡力系。这是质点系达朗贝尔原理的另一种表述。

二、惯性力系的简化

1、惯性力系的简化

对于任意运动的质点系，把实际受的力和虚加惯性力各自向任意点简化后所得的主矢、主矩分别记作和，于是，由力系平衡条件，得：

(1) 惯性力系的主矢

由质心运动定理有，得：

即，质点系惯性力的主矢恒等于质点系总质量与质心加速度的乘积，方向相反。

(2) 惯性力系的主矩

对任意固定点，由对任意固定点的动量矩定理有：

代入得：

对固定轴来说，将上式投影到任意固定轴上，得：

上式表明，质点系的惯性力对于任一固定点（或固定轴）的主矩，等于质点系对于该点（或该轴）的动量矩对时间的导数，并冠以负号。

对质心点来说，利用相对于质心的动量矩定理，可以得到质点系的惯性力对质心的主矩表达式：

对于质心轴来说，上式对通过质心的某一平移轴上的投影表达式为：

上式表明,质点系的惯性力对质心（或通过质心的平移轴）的主矩，等于质点系对质心（或该轴）的动量矩对时间的导数，并冠以负号。

2、刚体在各种常见运动情况下惯性力主矢和主矩的表达式

(1) 刚体做平移

刚体平移时，惯性力系一般向质心简化，主矢为：

主矩：

刚体平移时，惯性力系简化为通过刚体质心的合力。

(2) 刚体做定轴转动

刚体做定轴转动时，惯性力系向转轴上一点简化，设刚体绕固定轴转动，在任意瞬时的角速度为，角加速度为，主矢为：

设质心的转动半径为，则和的大小可以分别表示为：

其中：

显然，当质心在转轴上时，刚体的惯性力主矢等于零。刚体定轴转动时，惯性力系向固定轴简化，得到的惯性力系主矢的大小等于刚体质量与质心加速度大小的乘积，方向与质心加速度方向相反。

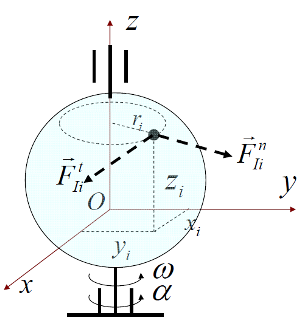
对于主矩，有：

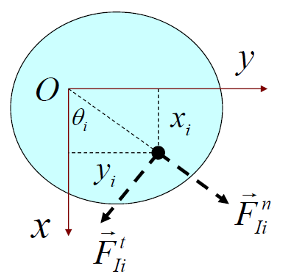
如图，有，所以化简有：

规定为对于轴的惯性积，则：

同理：

接着，对于：

如果刚体有质量对称面且该面与转动轴垂直，简化中心取次平面与转轴的交点，则：

当具有质量对称面的刚体绕垂直于这个平面的固定轴转动时，惯性力系向这个对称面与转轴交点简化的结果是作用在点的一个力和一个力偶。合力的矢量即为惯性力系的主矢，其大小等于刚体质量与质心加速度大小的乘积，方向与质心加速度方向相反。合力偶的力偶矩即为惯性力系的主矩，其大小等于刚体对转动轴的转动惯量与角加速度的乘积，方向与角加速度方向相反。

(3) 刚体做平面运动

此处的平面运动考虑为具有质量对称平面的刚体作平面运动，并且运动平面与质量对称平面互相平行。

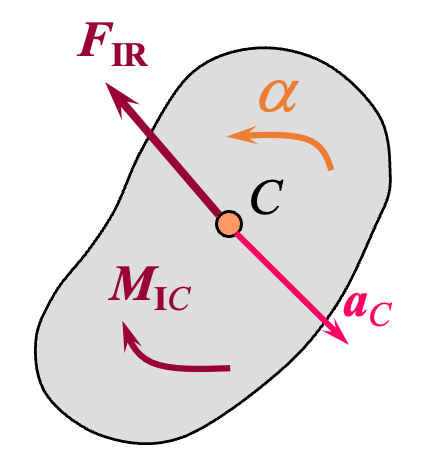
若取质心为基点，则刚体的平面运动可以分解为随质心的平移和绕质心（通过质心且垂直于运动平面的轴）的转动。故可向质心简化。

对于主矢计算，合力的矢量即为惯性力系的主矢，其大小等于刚体质量与质心加速度大小的乘积，方向与质心加速度方向相反：

对于主矩计算，惯性力系对质心的主矩等于刚体对通过质心的转动轴的转动惯量与角加速度的乘积，方向与角加速度方向相反：