一、光速
在真空中:
在介质中:
即:
其中
二、光的多普勒效应
当光速远大于源与观察者之间的相对速度
对于源远离观察者运动,公式为:
当
对于源远离观察者运动,公式为:
对于源靠近观察者运动,公式为:
由于频率和波长满足
对于源远离观察者的情况(红移):
对于源靠近观察者的情况(蓝移):
其中
三、光的色散
质的折射率
不同波长的光在同一介质中,折射率不同,导致传播速度不同:
其中
其中
由于
因此:
四、惠更斯原理
惠更斯原理是指每一个波前上的点都可以看作是新的“子波源”,每个子波源会向前发射一个新的球面波(或在二维情况下为圆形波)。经过一段时间后,所有这些子波的包络面就构成了新的波前。
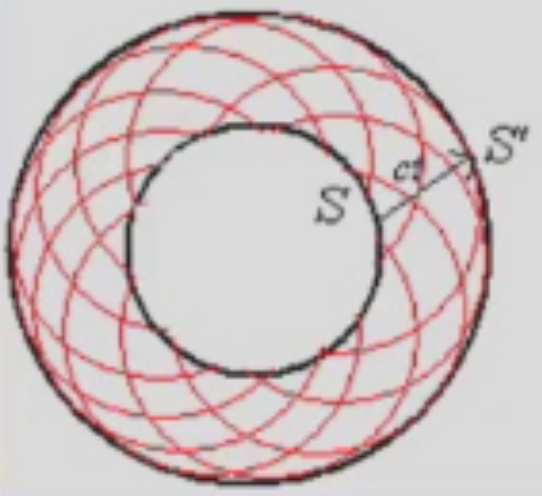
假设有一个初始波前
新波前
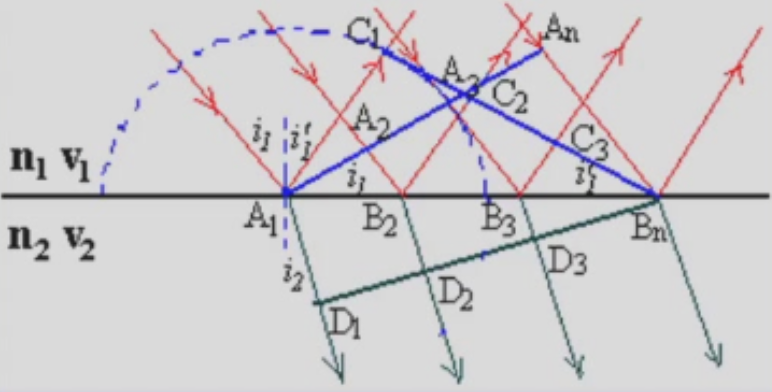
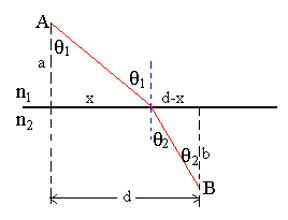
上图中上半部分是介质1(折射率
即,反射角等于入射角,这就是反射定律。
关注折射波前:
介质的折射率
所以:
这就是斯涅尔定律(折射定律)。
五、费马原理
假设光从点
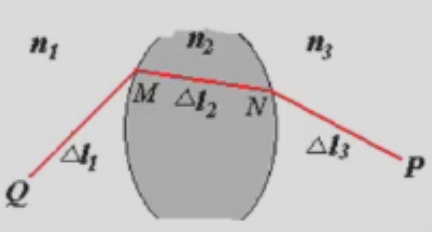
如图所示,光从
代入
光程是描述光在不同介质中传播路径的一种物理量,它与光的传播时间和速度有关。光程定义为光在各段介质中传播相当于在真空中传播的等效距离:
或在路径
对于任意曲线路径,从
其中,
也就是说,光线从一个固定点传播到另一个固定点时,其路径遵循这样的原则:与邻近路径相比,所需时间要么最短,要么最长,要么保持不变(即处于稳态)。用这个原理可以推导出光的入射和反射定律:
对于反射:
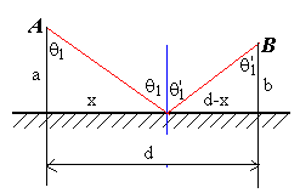
对于折射:
六、球面镜成像
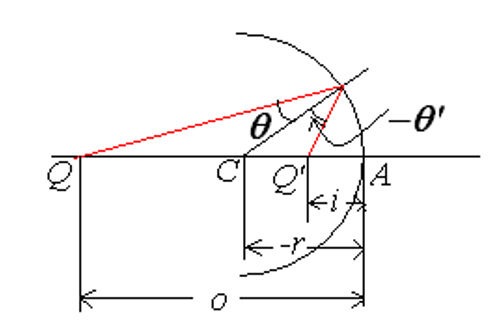
1、球面折射成像
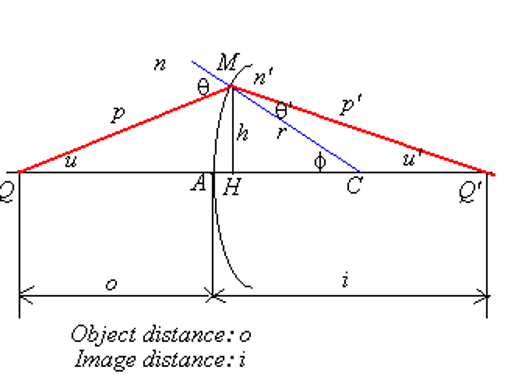
图中展示了一个球面折射问题:一个物体位于球面一侧,经过球面折射后在另一侧成像。已知:物体到球心的距离为
如图,
其中:
且有:
三角关系代入,得:
利用余弦定理:
利用
联立,将
这说明,实际情况下,物点
公式右边为零时:
即:
这两个条件只在特定的
实际成像分析时,通常只考虑靠近光轴的光线(即
进一步化简:
再整理得:
这是球面折射的傍轴成像公式。根据上面的公式,我们可以得到第一焦点(第一主焦点)当像距
那么第二焦点(第二主焦点)为:当物距
同样可以推导出焦距转换公式:
以及近轴成像公式(焦点形式):
这是球面折射(单面透镜)在近轴近似下的经典成像公式,也是实际光学设计中的基本公式。
NOTE
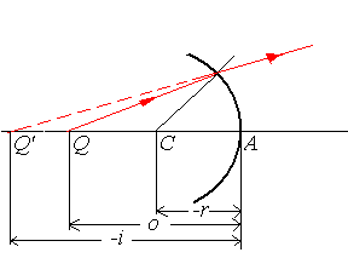
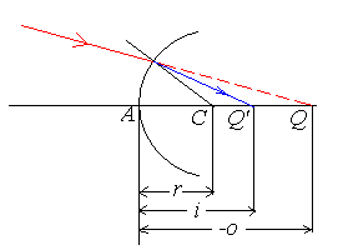
根据上面图示,做出符号约定:
| 位置关系 | 符号 | 说明 |
|---|---|---|
| Q 在 A 左(实物) | 物距为正 | |
| Q 在 A 右(虚物) | 物距为负 | |
| Q’ 在 A 左(虚像) | 像距为负 | |
| Q’ 在 A 右(实像) | 像距为正 | |
| C 在 A 左(凹面) | 曲率半径为负 | |
| C 在 A 右(凸面) | 曲率半径为正 |
下面两图为例:
2、球面反射成像
如果
通用焦点公式
将数据代入公式:
化简得:
这是在凹面情况下的成像公式。
3、傍轴物点成像和横向放大率
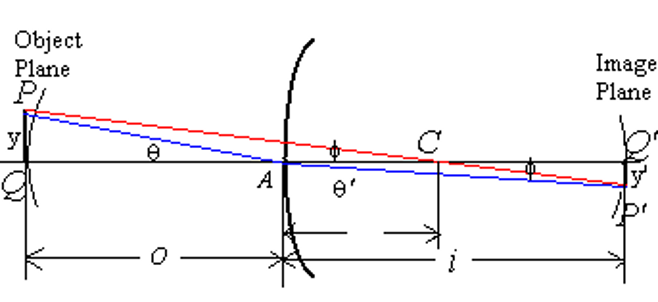
根据上图,在光学系统中,傍轴光线指的是距离光轴很近,且与光轴夹角很小的光线,其数学表达为:
其中
横向放大率定义为像点与物点高度之比:
对于折射(或透镜):折射前:
所以:
对于反射,介质折射率不变,
所以可以作出如下总结:
4、复合光学系统的成像(多透镜/多球面系统)
复合光学系统通常包含多个折射面(如多透镜、多球面),每个面都可能有不同的介质折射率。 如图:
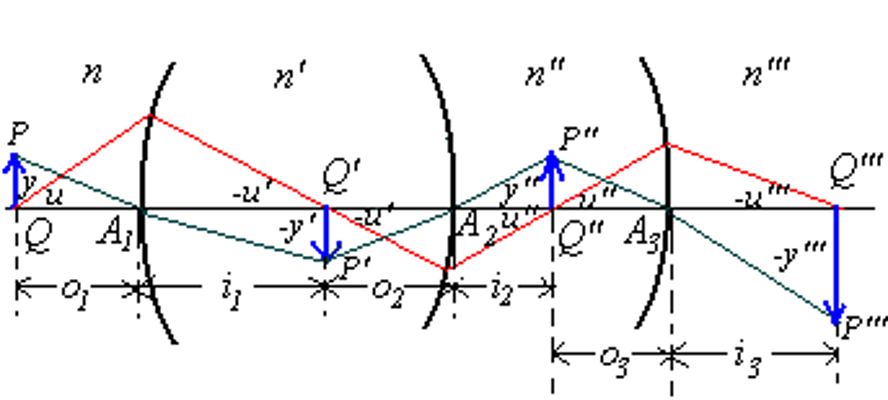
- 物点
- 各面折射率分别为:
- 各面前后物距、像距依次为:
- 各曲面半径:
对于每一个折射面(球面),应用折射公式:
- 第1面
- 第2面
- 第3面
对于每一面,也可写作透镜公式:
每一面对应的横向放大率为:
物点高度
经过第一折射面后的角度
所以:
如果将所有面连乘,总放大率为:
这里给出拉格朗日-亥姆霍兹不变量:
其中,
七、薄透镜成像
1、焦距计算
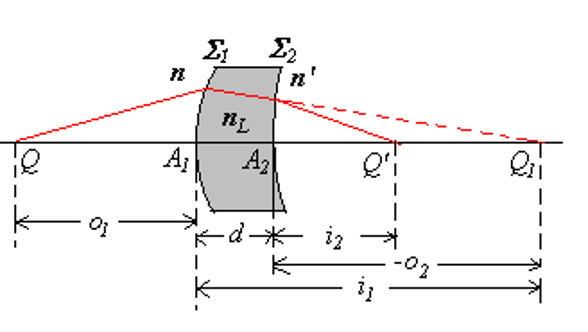
薄透镜是指厚度
对于球面
对于球面
每一面可定义主焦距(以前后介质为基准):
由图中:
其中
对第二面:
消去中间变量,得到:
当
其中,
2、磨镜者公式
下面推导磨镜者公式,其描述了透镜的焦距与其材料折射率以及两面曲率半径的关系。根据上面推导的公式:
得到像方焦距
将
化简分子分母,得到:
进一步整理,常用形式为:
类似地,物方焦距
代入并化简:
由于焦距间关系通常有
在空气中的薄透镜(
根据上面的推导,我们规定,如果
3、牛顿成像公式
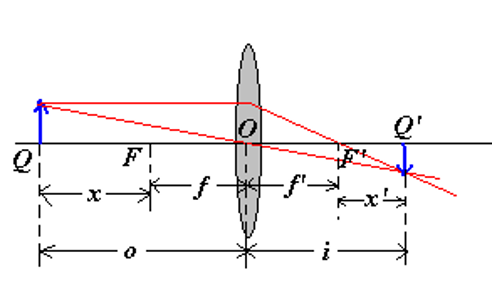
对于上图我们规定:
带入公式:
经过整理,得到牛顿公式:
4、横向放大倍数
横向放大率

对于第一折射面
对于第二折射面
总横向放大率为两面的乘积:
代入上式:
利用
对于空气中薄透镜(
利用牛顿公式
定义屈光度是焦距的倒数(以米为单位),可以用来去解决生活中的相关问题:
