一、电容

1、电容的定义

电容器由两个空间上分离的导体组成，分别可以带电为和。电容定义为电容器一个导体上所带电荷与两个导体之间电势差的比值：

电容只与电容器本身有关，与电荷和电压无关，它取决于极板的形状、相对位置以及填充在极板之间的材料。

2、不同类型电容器电容的计算

(1) 平行板电容器

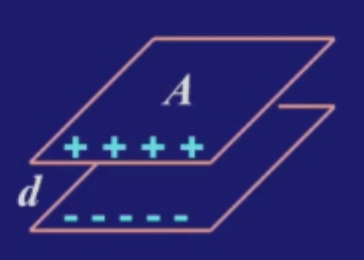
上面平行板电容器的上下表面分别带电，电势差为，两板之间的距离为。首先写出电容的计算式：

设电荷面密度：

列出电势差的计算公式：

根据高斯定理中推导的结论，平行板电容器内部的电场为：

将电场代入上面几式，得到：

所以，平行板电容器电容的大小只与两板面积和两板之间的距离有关。

(2) 圆柱形电容器

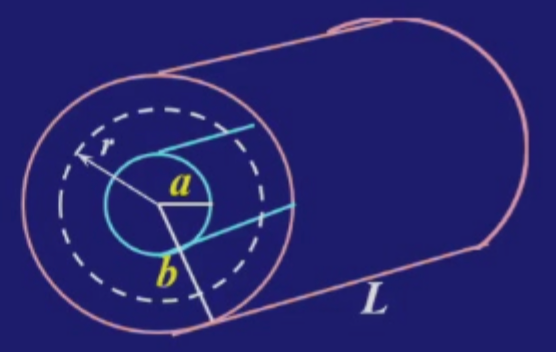
上面圆柱形电容器的内外部分分别带电，内圆柱半径为，外圆柱半径为，电势差为。构造一个圆柱面为高斯面，其半径为，长度为，其中半径要大于外圆柱的半径，运用高斯定理：

得到：

再列出电势的计算公式：

回代到电容计算公式：

(3) 球形电容器

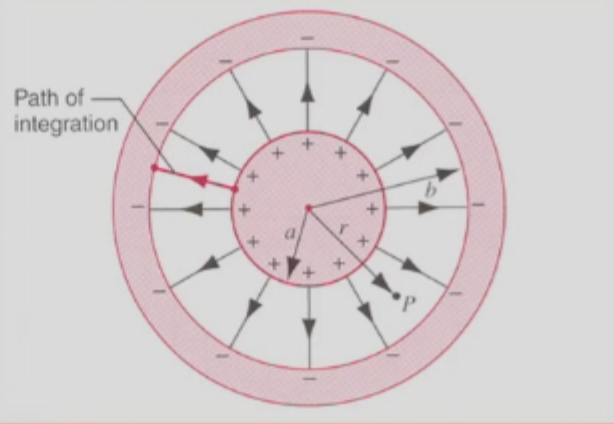
上面球形电容器的内外部分分别带电，内球的半径为，外球的半径为，电势差为。首先写出在电容器内部的电场公式：

代入电势的计算公式：

得出电容的计算公式：

考虑极限情况，当时，上式结果为：

也就是说，一个导体球也可以看成是一个球形电容器，其电容大小如上。

3、电容器的串并联

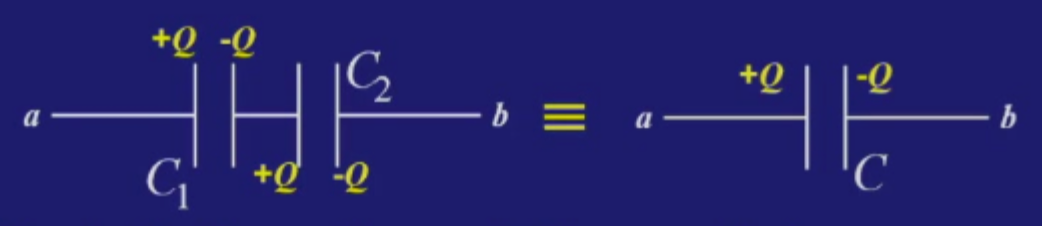
对于两串联电容器，其等效电容的计算：

所以：

对于两并联电容器，其等效电容的计算：

所以：

4、电容器的能量

首先假想两个平行板，不带电，将其中一个板的正电荷移动到另一个板，当移动的电荷，需要做的功为：

然后进行积分：

最终得到：

表示电容器所储存的能量，能量储存在电场本身中。可以把给电容器充电所需的能量看作是产生电场所需的能量。为了计算电场中的能量密度，首先考虑由平行板电容器产生的恒定电场：

化简电容器的能量公式：

联立两式，得：

所以电容器产生的电场能量密度（单位为）为：

其中为平行板电容器中的电场的体积。事实上，上面的能量（密度）公式是普适的，在非平行板电容器中，该结论依旧成立。

针对圆柱形电容器的能量证明：

二、电介质

1、电场中的绝缘体

在电容器的极板之间插入一种非导体材料（绝缘体）会改变电容器的电容值。为了研究这个特性，我们定义介电常数，材料的介电常数（介电常数）是指填充该材料时电容器的电容与未填充时的电容之比：

其中为真空作为介质的电容大小，是相对介电常数。真空的介电常数为，故恒成立。

将上面公式代入到不同种类的电容计算公式中得出：

• 平行板电容器电容：

• 圆柱体电容器电容：

• 球体电容器电容：

2、电介质作用原理

对于电容器内放置导体，如下图：

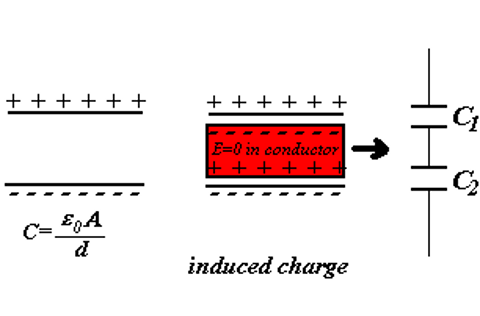
由于导体的性质，产生感应电荷，可以将原电容器看作是两个电容器，使用如下公式推导：

对于电容器内放置绝缘体，如下图：

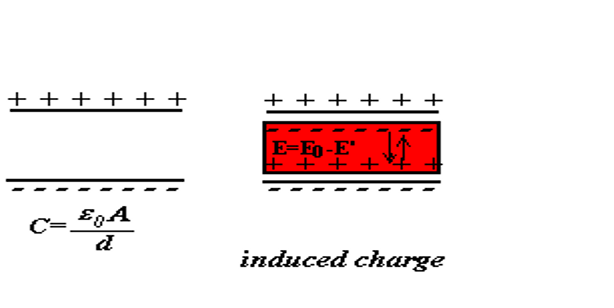
由于极化作用，绝缘体的分子在电场的作用下发生变化，产生了束缚电荷，束缚电荷产生的电场，抵消了一部分原来的电场，使用下面的公式推导结论：

3、极化强度矢量

定义极化强度矢量，用来描述电介质在外电场作用下内部产生的电偶极矩的强度和方向。极化强度矢量是单位体积内电偶极矩的总和，其定义公式为：

为单个分子或原子形成的电偶极矩。为单位体积。在均匀介质中，满足：

其中为单位体积内的分子数量，为每个电偶极子上的有效电荷量，为电偶极矩两电荷之间的距离。这也是位移极化的表达式。

现在探究极化强度矢量与导体面电荷密度之间的关系。考虑电介质表面区域的一小块面积，我们要计算这一块面积中所包含的电荷。由于极化后的内部形成了电偶极矩，每个偶极矩的正、负电荷互相抵消，而在电介质表面会出现净电荷。这一净电荷由极化向外“推出”（或收缩）并集中于电介质表面。感应电荷的面电荷密度可以定义为单位面积上的净电荷量为：

设极化强度为 ，其方向表示电偶极矩的方向。一个微面积 上的总感应电荷由极化强度的法向分量决定。设表面的法向单位矢量为 ，那么通过这一面积的极化总电荷为：

这里， 表示极化矢量在法向上的分量。所以单位面积上的感应电荷密度为：

这个公式表示电介质表面感应电荷密度 是极化强度矢量 沿表面的法向分量。

4、退极化场

(1) 退极化场现象

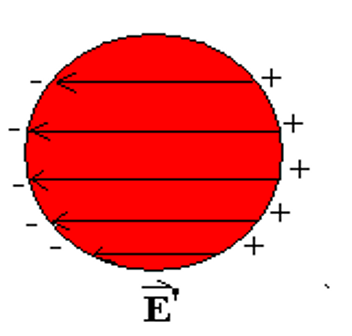
退极化场是电极化介质内部的一种特殊电场，其来源于极化介质表面或体内的束缚电荷产生的电场。

当一个绝缘体（电介质）受到外电场作用时，分子或原子内部的电荷分布会发生变化，导致电介质产生极化，形成极化强度 。极化会导致以下结果：

• 表面束缚电荷：极化使得介质表面上的电荷分布变得不均匀，形成束缚电荷。

• 体内束缚电荷：如果电介质内部存在极化梯度（即 ），则会在介质内部形成体电荷。

无论是表面束缚电荷还是体束缚电荷，它们都会产生电场，这个电场称为退极化场。退极化场与原磁场的叠加为（注意方向）：

(2) 退极化场计算

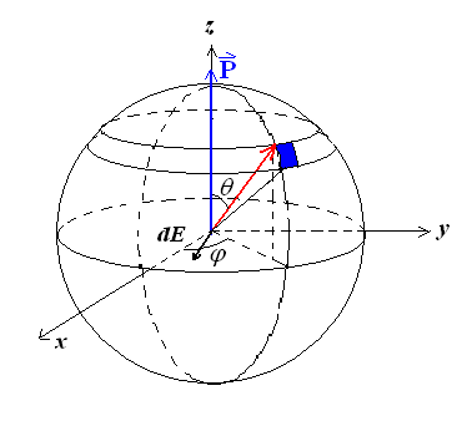
一个球形介质具有均匀极化强度 ，其表面电荷密度为：

其中 是球面上的点与极化方向 的夹角。我们需要计算球中心处的退极化场 。从球体的表面分布的电荷出发，考虑球表面微元面积 所产生的场强微元贡献 ：

• 球表面微元面积为：

• 表面电荷密度为：

• 微元电荷量为：

• 微元电场强度为（库仑定律）：

由于球对称性，退极化场的唯一非零分量位于极化方向（ 轴）。微元电场 在 方向上的投影为：

结合 的表达式：

退极化场 是整个球面电荷产生的场的叠加。我们对球表面进行积分：

将 的表达式代入：

积分中角度变量 和 是独立的，可以分离变量：

• 对 的积分：

• 对 的积分： 利用换元法，令 ，则 ，积分范围 对应 ：

计算 ：

因此：

将积分结果代入 表达式：

球中心处的退极化场为：

其中 是极化方向的单位矢量。

在平行板电容器中，可以直接使用高斯定理：

5、电介质的极化规律

对于各向同性的材料，存在如下公式：

其中为极化率，满足：

6、电感应强度

(1) 电感应强度的定义与性质

电感应强度，通常记为 ，是电介质中用来描述电场与极化效应的一种矢量场。

电感应强度 被定义为：

在电介质内部，使用高斯定律：

其中 是总电荷，包括自由电荷 和束缚电荷 。而极化强度 的高斯定律形式为：

自由电荷 与束缚电荷 的关系使得电场 和极化 的贡献可以分离。将电场强度 和极化强度 的贡献相结合，我们得到电感应强度 的高斯定律：

该公式表明，电感应强度 的通量仅与自由电荷 有关，而不受束缚电荷 的影响。

另外，在均匀介质中，可以利用电介质的极化规律，继续化简：

(2) 电感应强度的计算

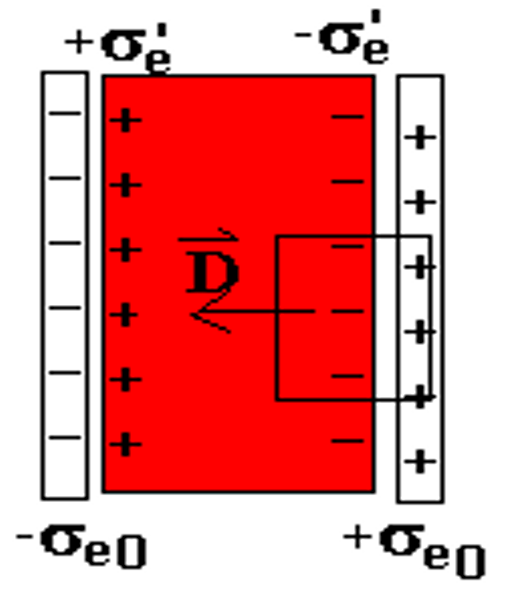
对于平行板电容器，在其中放置一个均匀导体介质，计算其电场。

l.