一、力的功

1、前面的你都会

2、作用于刚体力系的功

(1) 平移刚体上力的功

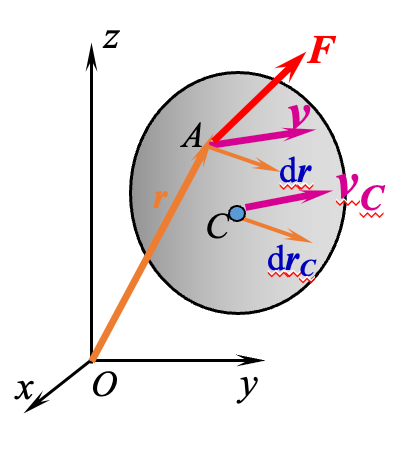
设一刚体在力 作用下作平移，其质心在 点，刚体上点 的矢径是 ，速度是 ，则力 的元功为：

或者

总功表达式为：

或者

(2) 定轴转动刚体上外力的功

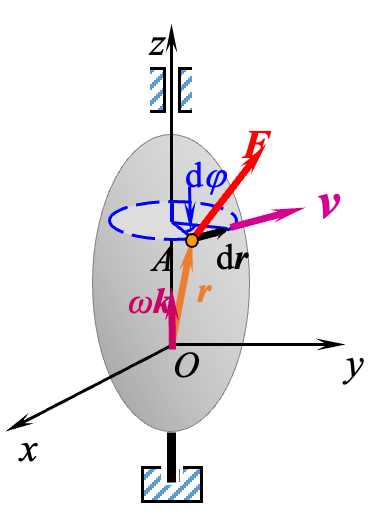
设刚体绕定轴 转动，角速度 ，刚体上点 的矢径是 ，速度是 。作用着力 ，当刚体有一微小转角 时，力 的元功为：

混合积表达式为：

由静力学知，力 对点 的矩矢

而力 对轴 的矩

等于 在轴 上的投影，即：

所以，混合积：

因此有元功：

总功为：

即作用于定轴转动刚体上的力的功，等于该力对转轴的矩与刚体微小转角的乘积的积分。特别是，若力矩是常量，则力在上述过程中的总功为：

(3) 平面运动刚体上力的功

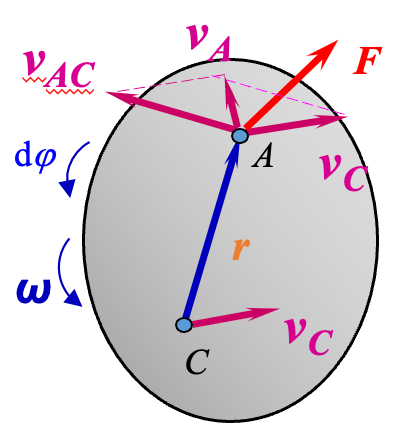
设一刚体在力 作用下作平面运动，其质心在 点，速度是 ，刚体上点 的速度是 ，则力 的元功表达式为：

其中 是 相对于质心 的速度。继续展开：

又因为 ，，所以

，其中 是力 关于质心 的矩在垂直于运动平面的分量，所以：

总功表达式即为：

即，作用于平面运动刚体上的力的功，等于该力在刚体随质心平动中的功与力对质心的矩在刚体转动中的功之和。力系可向刚体上任一点简化，都有类似结论成立。

(4) 质点系和刚体内力的功

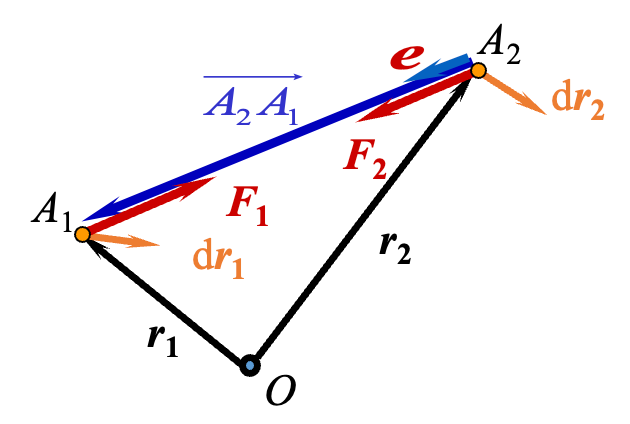
设质点系内有两质点 和 ，相互间作用着内力 和 ，且 。两质点的元位移分别是 和 ，故得内力 和 的元功之和：

由于 ，代入得：

引入矢量 ，设其单位矢量为 ，有：

所以

设：

由之前结论进一步推导：

其中，为单位矢量，有：

故上式中，第二项为零：

所以：

因此，元功之和为：

这里 代表两质点间距离 的变化量，在一般质点系中，两质点间距离是可变的，因此，可变质点系内力所作功的总和不一定等于零。但是，刚体内任意两点间的距离始终保持不变，所以刚体内力所作功的总和恒等于零。

(5) 约束力的功之和等于零的情形

1. 光滑的固定支承面和活动支座 的约束力总是和它作用点的元位移 垂直，所以这些约束力的功恒等于零。
2. 由于柔绳仅在拉紧时才受力，而任何一段拉直的绳子就承受拉力来说，都和刚杆一样, 其内力的元功之和等于零。
3. 光滑活动铰链内力元功之和等于零。
4. 圆轮沿支承面纯滚动时，摩擦力（约束力）的功为零。

二、动能

1、前面的你都会

2、平面运动刚体的动能

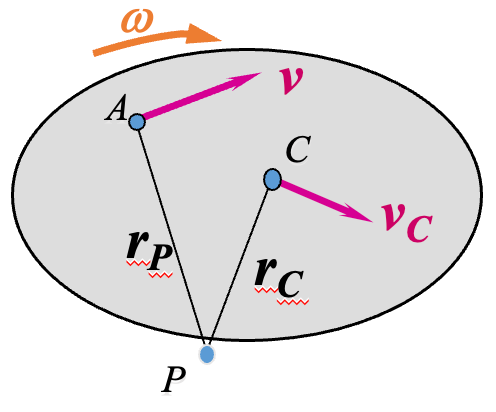
刚体做平面运动时，其上任一点的速度为 ，平面运动刚体的角速度是 ，速度瞬心在 点，刚体对瞬轴的转动惯量是 。对平行于瞬轴的质心轴的转动惯量是 ，则该刚体的动能为

设刚体的质心 到速度瞬心 的距离是 ，刚体的质量是 。根据转动惯量的平行轴定理：

有：

因为质心 的速度大小：

由上式得：

即，平面运动刚体的动能，等于它以质心速度作平移时的动能与相对于质心轴转动时的动能之和。为刚体质心时该公式才成立。

3、柯尼希定理

见文章柯尼希定理 (König’s Theorem) 。

三、动能定理

1、质点动能定理

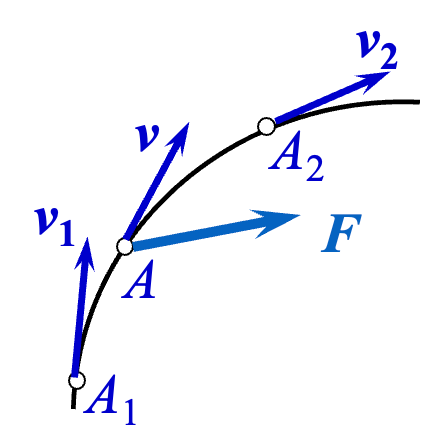
设质量为 的质点 ，在力 作用下沿曲线由 运动到 ，它的速度由 变为 。由牛顿第二定律：

即：

两边点乘速度 ，得：

上式右端就是作用力的元功，左端可改写成：

从而得：

即，质点动能的微分等于作用于质点上的力的元功，这就是质点动能定理的微分形式。

将上式沿路径 积分，得

式中 表示力 在路径 中的功。可见，质点动能在某一路程中的改变量，等于作用于质点的各力在该路程中所作的功。这就是质点动能定理的积分形式。

2、质点系动能定理

对于质点系中的每个质点，都有质点动能定理的微分形式，相加得：

由于：

所以：

即，质点系动能的微分等于作用于质点系各力的元功的代数和，这就是质点系动能定理的微分形式。

由微分形式，将上式积分，得到：

式中，分别代表某一运动过程中开始和终了时质点系的动能。上式表明质点系的动能在某一路程中的改变量，等于作用于质点系的各力在该路程中的功的代数和。这就是质点系动能定理的积分形式。