一、拉普拉斯变换

1、拉普拉斯变换的定义

傅里叶积分和傅里叶变换的应用要满足以下两个条件：

1. 原函数定义域为。
2. 原函数在定义域区间上必须是绝对可积。

为了能让更多的函数能够应用傅里叶变换，我们构造一个新的函数：

通过引入阶跃函数后可以把函数延拓到整个实轴上，只不过在上的函数值为。后面内容将会省略函数。是一个正的实数，只要其取值足够大，总能保证在区间上时绝对可积的，把称为收敛因子，对于一般的物理问题，都满足这个条件。

当函数除了在有限个第一类间断点外处处连续时，函数满足狄利克雷条件及绝对可积条件，从而 可以进行傅里叶变换与逆变换：

引进一个新的变量： 及新的函数

其中积分称为拉普拉斯积分，称为的拉普拉斯变换函数。代表着从到的一种变换，称为拉普拉斯变换，称为拉普拉斯变换的核。

的傅里叶逆变换是：

即：

由 ,有 ，所以：

又称为像函数，而称为原函数，它们之间的关系常用简单的符号写为：

使用拉普拉斯变换存在的条件：

1. 原函数最多只有有限个第一类间断点，在其他点上都是连续的。
2. 原函数有有限的增长指数。也就是说，存在正数 及非负的实数（称为增长指数），对于任何满足：

那么拉普拉斯变换在半平面上存在，而且在此半平面内，像函数就是函数。这是拉普拉斯变换存在的充分条件。显然，有下确界，称之为绝对收敛横标。

2、拉普拉斯变换的性质

(1) 线性性

(2) 解析性

该函数是解析的，所以求导数和求积分可以交换次序。

(3) 导数定理

1. 一阶导数性质：

证明：

2. 高阶导数性质：

上式通过一阶导数性质递推可得。

(4) 积分性质

证明：

利用拉普拉斯变换性质代入即可。

(5) 相似性质

相似即为在时间尺度上进行缩放：

证明：

令，有：

(6) 位移性质

位移表示在频率域上进行平移：

证明：

令，有：

(7) 延迟性质

延迟表示在时间域上平移：

证明：

(8) 卷积性质

证明：

这道积分是先固定对进行积分，再对进行积分，我们可以改变积分次序，得到：

(9) 初值定理

如果函数拉普拉斯变换存在， 而且当时 的极限存在，那么有：

证明不作要求。

(10) 终值定理

如果函数拉普拉斯变换存在， 而且当时 的极限存在，那么有：

证明不作要求。

(11) 我也不知道叫什么名字的定理

当 时， 有界，那么：

(12) 第二个我也不知道叫什么名字的定理

如果函数的拉普拉斯变换存在，则：

对拉普拉斯变换的定义式两边求导即可。

二、拉普拉斯变换的反演

拉普拉斯变换主要用于求解线性微分方程(或积分方程)。对原方程进行拉普拉斯变换后，可以得到像函数所遵从的代数方程，求解代数方程得到像函数，然后再把像函数还再回到原函数，称为拉普拉斯变换的反演。

反演的唯一性问题：如果两个函数的拉普拉斯变换相同，而且这两个函数是连续的，那么这两个函数必定相等。根据反演的唯一性，我们可以利用前面拉普拉斯变换的性质来求像函数反演的结果。

1、有理分式反演法

如果像函数是有理分式，只要将有理分式进行因式分解，然后利用拉普拉斯变换的一些基本性质就能得到相应的原函数：

2、查表法

根据延迟定理、位移定理和卷积定理，配合拉普拉斯变换表解决反演问题。

3、黎曼-梅林反演公式法

这里是大于收敛横标任意正数。积分路径是 平面上与虚轴平行的一条直线。像函数是的解析函数，可以借助于留数定理来求该积分的主值。该反演公式在原函数的连续点收敛到原函数的值，在间断点收敛到左右极限的平均值。

构造辅助围道（围道内函数解析），右边直线上积分与要求的积分相关，是以原点为圆心，半径为的圆，使得像函数的所有奇点都包含在该围道内所围成的区域内。

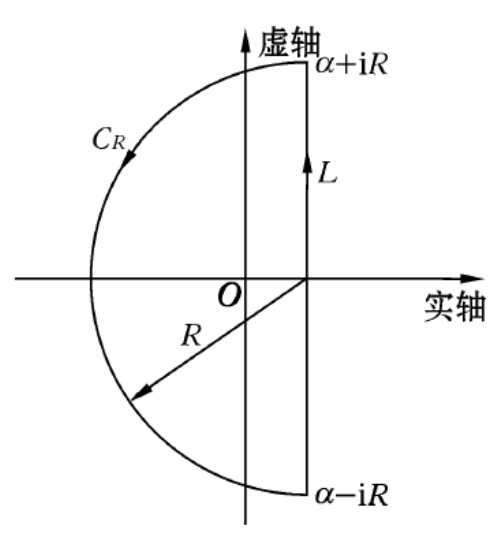
根据推广的约当引理，当半径趋向于无穷大时，沿上的积分值趋向于零，应用留数定理，求得上面黎曼-梅林反演公式的值为：

当是多值函数时，为了应用留数定理积分路径需要做一些修改，保证积分只在某单值分支上进行。

三、 拉普拉斯变化应用

1、求解常微分方程

(1) 非线性二阶常微分方程

例：对于非线性二阶常微分方程：，可以对方程两边进行拉普拉斯变换：

利用拉普拉斯的导数性质，记：，得到：

带回方程，得到：

求逆变换，利用拉普拉斯的卷积性质，得：

(2) 变系数常微分方程

例：对于变系数常微分方程：

记：，两边进行拉普拉斯变换：

化简得到：

由于：

可以对化简之后的方程两边求拉普拉斯逆变换：

使用常微分方程求解方法求解，得到答案：

2、求解积分方程

例：对于方程，两边进行拉普拉斯变换，利用卷积性质，得到：

解得：

求逆变换，得到：

3、求解LR回路问题

例1：

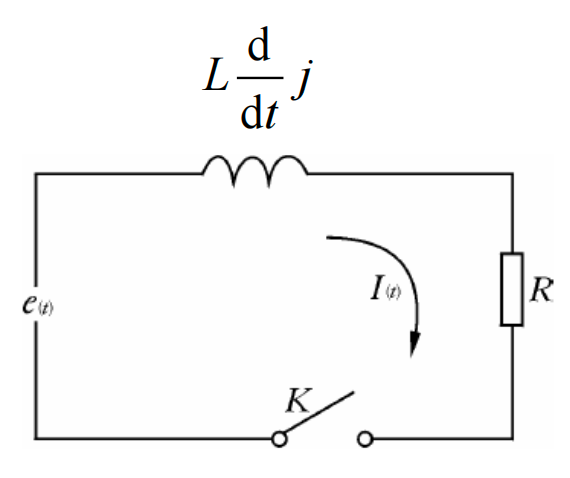
在如图所示的LR电路中，交变信号源为，在时刻合上电源，求电流变化规律。

解1：根据基尔霍夫电压定律，电流所要满足的电流：

对方程两边进行拉普拉斯变换，记：

移项求解：

利用拉普拉斯变换的卷积性质，逆变换得到：

将后面的积分求解，使用分部积分法，得到：

例2：

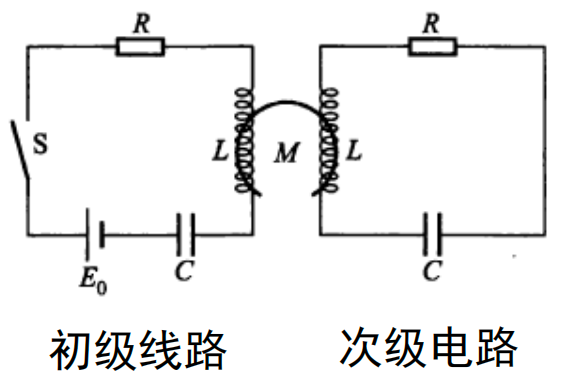
如图所示，两个线圈具有相同的（电阻），（电感）和（电容），线圈之间互感系数为。初级线路有电压为的直流电源。现在接通初级线路中的开关， 问次级电路中电流的变化情况如何？

解2：根据基尔霍夫定律，初级电路满足：

次级电路满足：

初始条件为：。

对方程进行拉普拉斯变换，设得：

求解得：

配方、利用拉普拉斯变换的平移性质，进行拉普拉斯逆变换，解得：

4、求解弹簧-质量-阻尼系统的强迫振动问题

例：

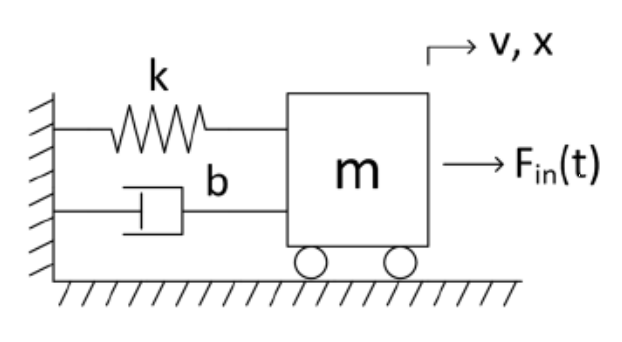
求解方程：

解：

记，对方程两边进行拉普拉斯变换，得：

求解得：

求拉普拉斯逆变换：

由答案可知，该系统的频率为。