一、电磁波的产生
1、静止电荷
当一个电荷静止时,它只在空间周围产生静电场
其中,
2、匀速运动的电荷
当一个电荷以恒定速度运动时,它会产生恒定的磁场
其中,
3、加速运动的电荷
只有当电荷发生加速运动时(即速度随时间变化),如电流
4、LCR电路
LCR电路由电感(L)、电容(C)和电阻(R)串联组成。设电容上的电荷为
这是一个二阶线性齐次微分方程。该方程的通解为:
其中,
其中当
由于电阻的存在,能量会随着时间逐渐损耗。电荷的振荡会随时间指数衰减,
二、电磁波的传播
当一个电偶极子(如天线中的两极)发生振荡时,它会产生电磁辐射。偶极子的振荡电流随时间变化,通常为谐振荡形式:
这会导致偶极子周围的电场和磁场发生周期性变化,从而向外辐射电磁波。偶极子的辐射是线性极化的,即电场矢量的振动方向始终保持在一个固定的方向上——这个方向就是偶极子的轴向。例如,垂直偶极子的电场振动方向也是垂直的。这种极化方式在天线和无线电技术中非常常见。
偶极子的辐射强度在空间不同方向并不均匀,形成了特定的辐射方向图:
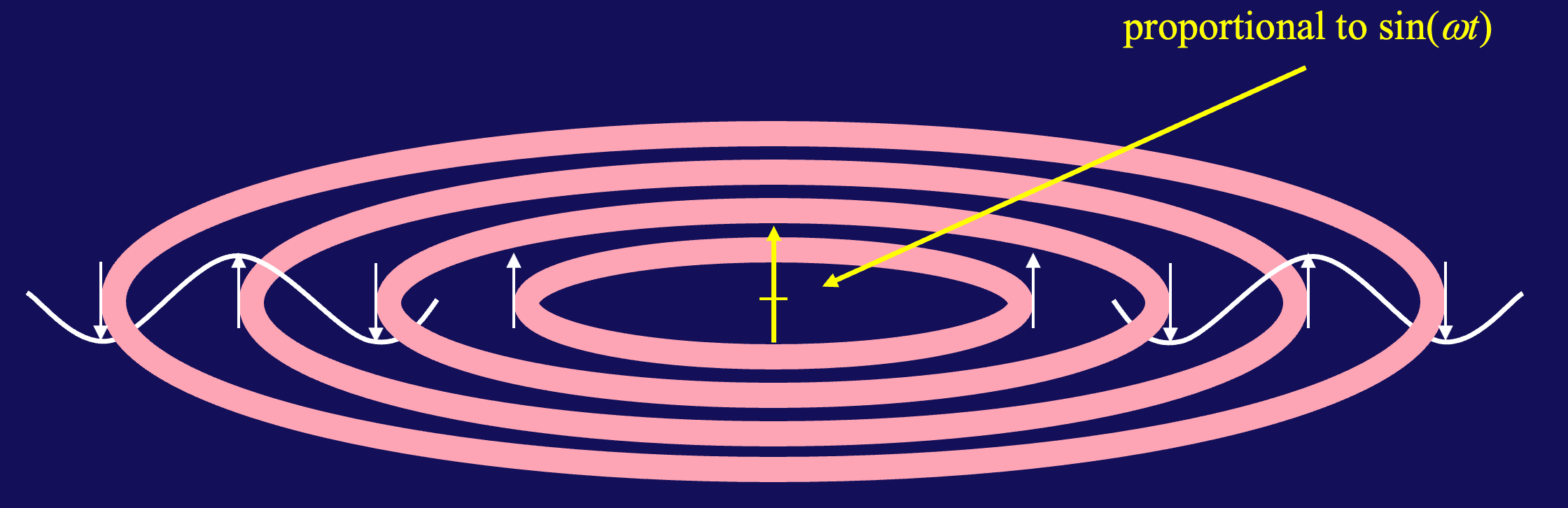
三、电磁波的性质
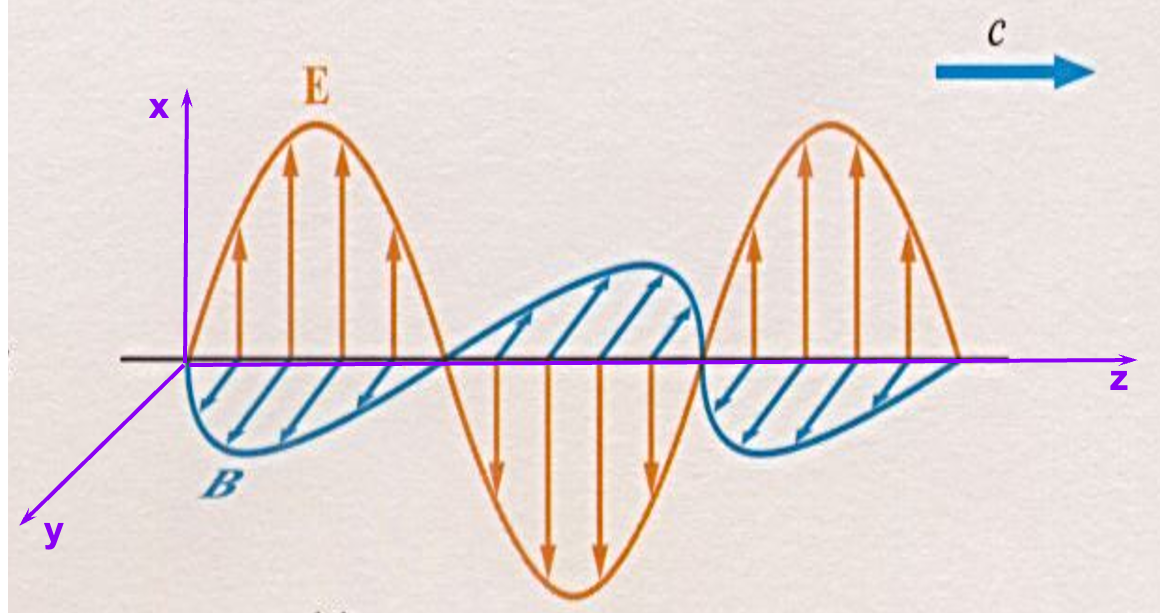
在距离波源较远的自由空间(
1、横波性质
电磁波是横波,即电场
电场、磁场和传播方向三者互相垂直,构成空间中的正交坐标系。
2、电场与磁场互相垂直
在电磁波中,电场
3、电场与磁场同相
电磁波中的电场和磁场变化同步,即同相:
在空间中某一点,电场和磁场的最大值、最小值同时出现。
4、右手定则
三者满足右手定则:用右手,拇指指向波的传播方向
5、电磁波的传播速度
电磁波在自由空间中的传播速度为:
其中
在真空或空气中:
6、振幅关系
磁场与电场的振幅存在以下关系:
四、麦克斯韦方程组求解
积分形式的麦克斯韦方程组:
自由空间下的麦克斯韦方程组(
将第一个方程和第二个方程的电场写成分量形式,为:
将第一个方程和第二个方程的磁场写成分量形式,为:
平面波是指电磁波在空间传播时,在任意与传播方向垂直的平面上,其相位(
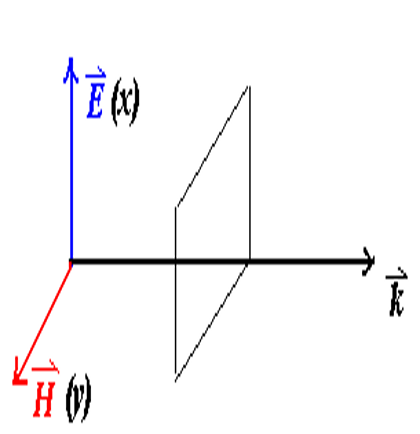
平面波条件下的麦克斯韦方程分量表达式,包括:
- 电场的散度方程
- 电场的旋度方程(各分量)
- 磁场的散度方程
- 磁场的旋度方程(各分量)
由于平面波假设
上述各式可以进一步简化为只含
磁场散度方程变为:
同时,根据电场和磁场的旋度方程,还可以得到:
说明
电场旋度分量可以进行化简:
磁场旋度分量化简为:
这里不妨设电场
说明在这种假设情况下,
将方程:
两边对
即:
同理,对于磁场:
根据数学物理方法相关知识,解得波动方程的常规解:
这里,
即
波相位为
定义波速
对于真空,波速即:
这就是光在真空中的速度。再次回到方程的常规解,取
方程右边分别对
带入第一个方程:
所以
消去公因子,移项:
联立波数与频率波速关系
而波速
即:
化简,得到:
由上面的解形式,
更一般地,可以写成:
如果考虑相位,则:
在真空中,结果为:
进一步,
或反过来,
于是,我们通过了麦克斯韦方程组求得了所有的电磁波的性质。
五、电磁波的能量
1. 电磁场的能量密度及总能量
在空间
其中,
在更一般的情况下,介质并非真空,需用电位移矢量
其中,
其中
在非稳态(即电场
2、波印廷矢量与电磁波能量转换
对时间求导,得到能量变化率:
对
一般写为:
麦克斯韦方程组给出:
带入能量变化率公式:
根据矢量恒等式:
所以:
将体积分换成闭合曲面积分(高斯定理):
最终能量变化率表达为:
第一项中的
其中:
或
其中
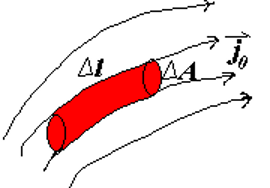
假设电流通过一个横截面积为
带入上一节表达式:
进一步整理:
其中
3、真空波阻抗
电磁波的能量传播方向由坡印廷矢量
对于自由空间(真空):
因此:
对于平面波(电场与磁场正交且大小恒定),电场和磁场的振幅分别为
又因电磁波中
定义真空波阻抗
则坡印廷矢量的大小可以简化为:
4、电磁波强度
强度
对于简谐(正弦)波,电场可写为
故
单位为
5、电磁波能量密度
电场的能量密度为:
磁场的能量密度:
结合
通常规定能量密度为上式的平均值,即:
其中
六、直流回路中的电磁波能量
虽然坡印廷矢量
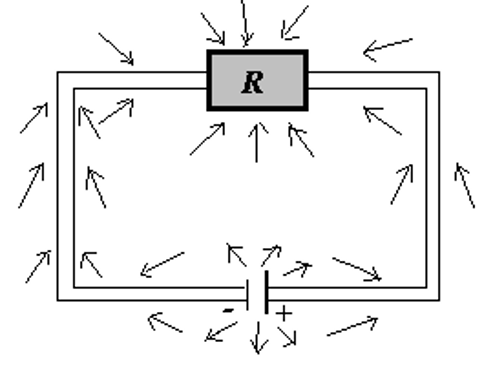
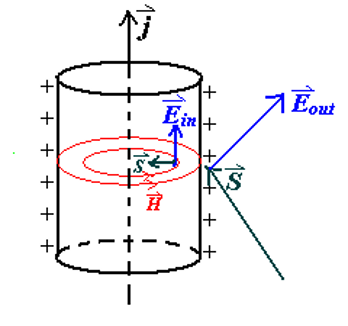
通常我们认为,电流沿导线内部流动,能量“跟着电流走”,从电源流向负载(电阻)。但电磁场理论告诉我们,能量其实是通过导线外部的电磁场,以坡印廷矢量的方向流动,从电源传输到电阻。具体来看,在导线附近,
七、电磁波的动量
电磁波传播时,除了能量流(坡印廷矢量
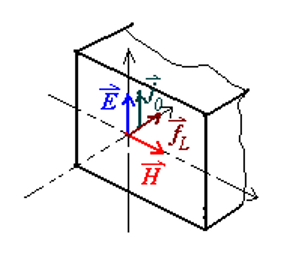
如图
即:
其中,
如果完全吸收,则
板获得的动量变化为:
电磁波在
入射波动量密度:
反射波动量密度:
动量密度的变化:
简化得:
于是得到电磁场的动量密度(任意时刻):
