一、刚体的平移

1、平移的定义

在运动过程中，刚体上任意一条直线的方向都保持不变。具有这种特征的刚体运动，称为刚体的平行移动，简称为平移。

2、平移的性质

当刚体作平移时，体内所有各点的轨迹形状完全相同，而且在每一瞬时，刚体各点的速度相等，各点的加速度也相等。

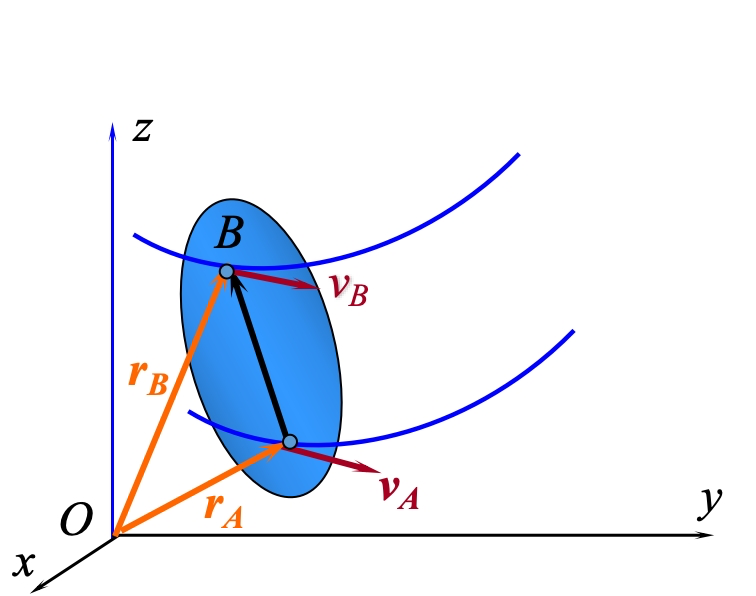
证明：

因为这是一个刚体，并且进行的是平移运动，所以刚体内任意线段的长度和方向都保持不变。因为：

两边求导得：

再求导一次，得出加速度相等。

应该注意，平移刚体内的点，不一定沿直线运动，也不一定保持在平面内运动，它的轨迹可以是任意的空间曲线。如果平移刚体内各点的轨迹都是平面曲线或直线，则这些特殊情形称为平面平移或直线平移。由上述定理可见，当刚体作平移时，只需给出刚体内任意一点的运动，就可以完全确定整个刚体的运动。这样，刚体平移问题就可视为点的运动问题来处理。

二、刚体的定轴转动

1、定轴转动的定义

当刚体运动时，如其上或其延展部分有一条直线始终保持不动，这种运动称为刚体的定轴转动。该固定不动的直线称为转轴。

2、定轴转动的特点

当刚体作定轴转动时，转动轴以外的各点都分别在垂直于转轴的平面内作圆周运动，圆心在该平面与转轴之交点上。

3、研究定轴转动的参数

(1) 角坐标

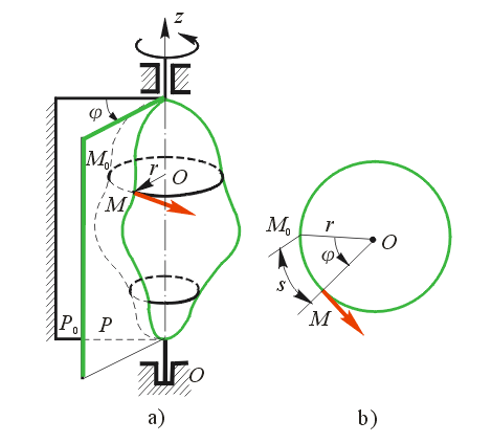
刚体的位置可以由角完全确定，称为角坐标，当刚体转动时，角坐标随时间变化，因此可以表示成时间的单值连续函数：

约定自轴的正端往负端看，从固定面起按逆时针转向计算角，取正值；反之为负。

(2) 角速度

角对时间的导数，称为刚体的角速度（代数值）以表示。故有：

角速度的大小表示刚体在该瞬时转动的快慢，即单位时间内转角的变化。当转角随时间而增大时，为正值，反之为负值，这样，角速度的正负号确定了刚体转动的方向。

(3) 角加速度

角速度对时间的导数，称为角加速度（代数值），以代表，故有

它表示单位时间内角速度的变化。

和正负相同，则角速度的绝对值随时间而增大，即刚体作加速转动；反之，两者正负不同，则角速度的绝对值随时间而减小，即刚体作减速转动。但减速转动只到时为止。 刚体由静上开始的转动都是加速转动。

三、刚体内各店的速度与加速度矢积表示

1、角速度与角加速度的矢量表示

(1) 角速度矢

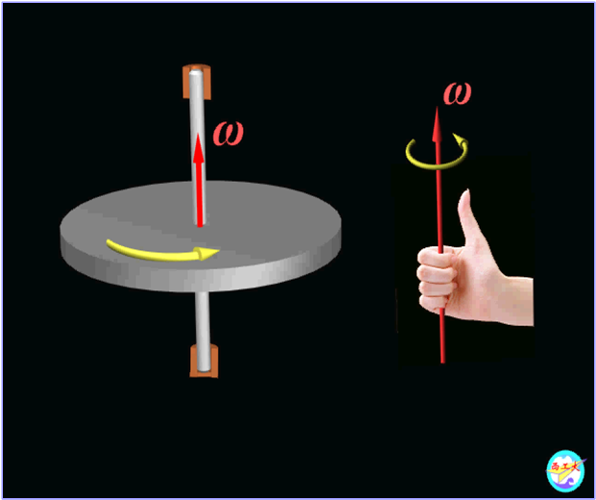
沿刚体的转轴画出一个矢量其中为轴的单位矢称为刚体的角速度矢。它的作用线表示出转轴的位置，而它的模则表示出角速度的绝对值。的指向由右手规则决定。定轴转动刚体的角速度矢被认为是滑动矢量，可以从转轴上的任一点画出。

(2) 角加速度矢

同样，可以用矢量表示刚体的角加速度，它也是滑动矢量，沿转轴画出。它的大小表示角加速度的模，它的指向则决定于的正负。

2、刚体内各点的速度与加速度矢积表示

(1) 速度矢积表示法

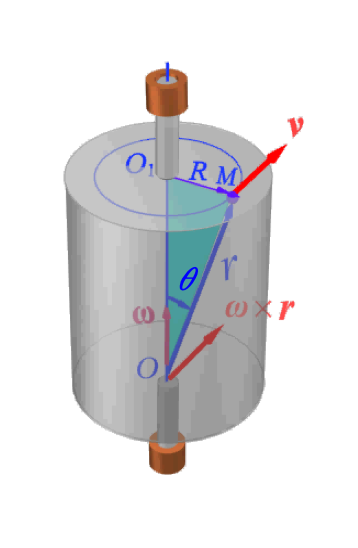
定轴转动刚体内任一点的速度的大小为。由于，因而。

根据矢积的定义，矢积的模也等于，它的方向也与速度的方向一致，故有矢积表达式：

定轴转动刚体内任一点的速度，可以由刚体的角速度矢与该点的矢径的矢积来表示。

(2) 加速度矢积表示法

将速度矢积表达式左右两边对时间求导数。左端的导数为点的加速度，而右端的导数为：

上式第一个矢积的模为：

此矢积垂直于由转轴和转动半径决定的平面，它的指向与图中自点画出的矢量一致。可见，矢积按大小和方向都与点的切向加速度相同。故有矢积表达式：

第二个矢积的模为：

此矢积同时垂直于刚体的转轴和点的速度，即沿点的转动半径，并且按照右手规则它是由点指向轴心。可见，矢积表示了点的法向加速度，即有矢积表达式：

附加证明：

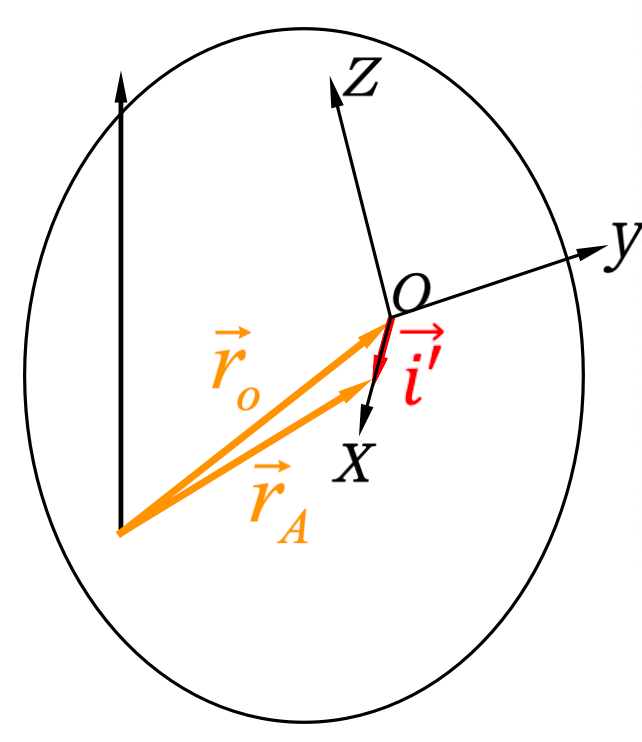
对于固结在刚体上的动坐标系 的单位矢量 （包括 , , ），它们在随体转动时相对空间（惯性系）点的时间导数，依据理论力学的旋转矢量表达式，有：

这是因为坐标系自身随刚体一起以角速度绕轴转动，单位矢量在空间中变化率等于和该单位矢量的叉乘。

同理，对于, 也完全相同：

这证明了三组单位矢量在刚体角速度作用下的导数关系，即动坐标系单位矢量对时间的导数为它本身。