一、全微分方程定义与性质

我们将一阶方程改写为对称的形式：

$$ M(x, y)\mathrm{d}x + N(x, y)\mathrm{d}y = 0 $$

如果上式的左边恰好是某一个二元函数 $u(x, y)$ 的全微分，即：

$$ M(x, y)\mathrm{d}x + N(x, y)\mathrm{d}y = \mathrm{d}u(x, y) $$

则称之为全微分方程，$u(x, y)$ 称为它的一个原函数。

设 $y = y(x)$ 是全微分方程的一个解，且 $y(x_0) = y_0$。则：

$$ M(x, y(x)) \mathrm{d}x + N(x, y(x)) \mathrm{d}y(x) \equiv 0 $$

即：

$$ \mathrm{d}u(x, y(x)) \equiv 0 $$

于是：

$$ u(x, y(x)) \equiv c_0 = u(x_0, y_0) $$

即 $y = y(x)$ 是 $u(x, y) = u(x_0, y_0)$ 满足 $y(x_0) = y_0$ 所确定的隐函数。反之，设$y=y(x)$是$u(x,y)=u(x_{0},y_{0})$满足$y(x_{0})=y_{0}$所确定的隐函数，则有：

$$ u(x,y(x))\equiv u(x_0,y_0) $$

求微分，得：

$$ \mathrm{d}u(x,y(x))\equiv 0 $$

于是：

$$ M(x,y(x))\mathrm{d}x+N(x,y(x))\mathrm{d}y(x)\equiv 0 $$

故$y=y(x)$是全微分方程的的解。

由以上论证可知，如果已知方程是一个全微分方程，$u(x,y)$是它的一个原函数，则：

$$ u(x,y)=u(x_0,y_0) $$

是方程满足条件：当$x=x_0$时$y=y_0$的积分，其中$(x_0,y_0)\in G$.并且

$$ u(x,y)=C $$

是方程的通积分，$C$是任意常数。
现在存在两个问题：

1. 如何根据$M(x,y)$和$N(x,y)$去判别方程为全微分方程。
2. 当方程为全微分方程时，如何去求原函数$u(x,y)$.

二、全微分方程的判别

为了判别一个方程是否为全微分方程，给出下面的定理：

设函数$M(x,y)$和$N(x,y)$在单连通区域$G$内连续且有连续的一阶偏导数，则方程为全微分方程的充要条件是：

$$ \frac{\partial M}{\partial y}\equiv\frac{\partial N}{\partial x},(x,y)\in G $$

一个区域$D$中，任一闭曲线所围区域，都属于区域$D$，称为“单连通区域”。这就意味着，区域$D$是实心的，不能有空洞。

三、全微分方程求解

1、方法一

当满足充要条件，确定方程为全微分方程时，可以由下述与路径无关的曲线积分求得一个原函数：

$$ u(x,y)=\int_{(x_0,y_0)}^{(x,y)}M(x,y)\:\mathrm{d}x+N(x,y)\:\mathrm{d}y $$

其中点$(x_0,y_0$)可以取$G$ 内任意一个定点。
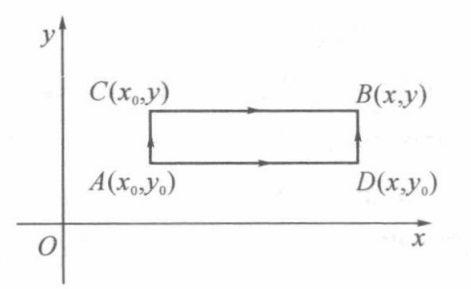
如果$G$是边平行于坐标轴的矩形区域，则从点($x_0,y_0$)到点$(x,y)$ 可取边平行于坐标轴的折线$\overline{AD}\cup\overline{DB}$或$\overline{AC}\cup\overline{CB}$

其计算公式为：

$$ u(x,y)=\int_{x_0}^xM(\xi,y_0)\mathrm{d}\xi+\int_{y_0}^yN(x,\eta)\mathrm{d}\eta $$

或：

$$ u(x,y)=\int_{x_0}^xM(\xi,y)\mathrm{d}\xi+\int_{y_0}^yN(x_0,\eta)\mathrm{d}\eta $$

2、方法二

我们也可以不使用曲线积分，采用下述不定积分的方法求原函数$u(x,y)$。因为：

$$ \mathrm{d}u(x,y)=M(x,y)\mathrm{d}x+N(x,y)\mathrm{d}y $$

所以：

$$ \frac{\partial u}{\partial x}=M(x,y),\frac{\partial u}{\partial y}=N(x,y) $$

由前一式，有

$$ u(x,y)=\int M(x,y)\mathrm{d}x+\varphi(y) $$

这里积分中把$y$看作常量，$\varphi(y)$是$y$的任意可微函数。再由第二式，有：

$$ \frac{\partial u}{\partial y}=\frac{\partial}{\partial y}\int M(x,y)\mathrm{d}x+\varphi'(y)=N(x,y) $$

由此求得：

$$ \varphi'(y)=N(x,y)-\frac{\partial}{\partial y}\int M(x,y)\mathrm{d}x $$

在方程为全微分方程的条件下，可证上式右边与$x$无关，从而可求出$\varphi(y)$，代入即得$u(x,y)$。

3、方法三

此方法的优点是不必事先验证该方程是否满足充要条件来判断是否为全微分方程，但难点是找原函数要采用“凑”的办法，有一点技巧，要熟练掌握求二元函数全微分的逆向思维。例如下面一些等式，从右到左是计算二元函数的全微分，而从左到右就是“凑”出原函数。

$$ y\mathrm{d}x+x\mathrm{d}y=\mathrm{d}(xy) $$

$$ \frac{y\mathrm{d}x-x\mathrm{d}y}{y^2}=\mathrm{d}\left(\frac{x}{y}\right) $$

$$ \frac{-y\mathrm{d}x+x\mathrm{d}y}{x^2}=\mathrm{d}\left(\frac{y}{x}\right) $$

$$ \frac{-y\mathrm{d}x+x\mathrm{d}y}{x^2+y^2}=\mathrm{d}\left(\arctan\frac{y}{x}\right) $$

$$ \frac{y\mathrm{d}x-x\mathrm{d}y}{x^2-y^2}=\mathrm{d}\left(\frac{1}{2}\ln\left|\frac{x-y}{x+y}\right|\right) $$