[alart]学习线段树,你需要先完成树、数组、分治思想、递归的学习(可以说是学习成本极低了)[\alart]
引入
线段树是一个用途极为广泛的数据结构,在提高组及以上的比赛中经常看到它的身影。
现在我有一个问题,给一个长度为 $n$ 的序列,我需要将序列中一个范围内的每一个数进行一次运算,例如加上 $x$ ,也就是区间修改,然后查询修改后一个区间范围内所有值的和或者其他量,也就是区间查询,连续进行几次操作,输出每次区间查询的结果。
现在给你们五分钟的时间,你们就能写出来。主要代码大概就是这个样子:
#include<iostream>
#include<cstdio>
using namespace std;
int a[10010],n,t,opt;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
scanf("%d",&t);
while(t--){
scanf("%d",&opt);
if(opt==1){
int x,y,k;
scanf("%d%d%d",&x,&y,&k);
for(int i=x;i<=y;i++)
a[i]+=k;
}
else{
int x,y,sum=0;
scanf("%d%d",&x,&y);
for(int i=x;i<=y;i++)
sum+=a[i];
printf("%d\n",sum);
}
}
system("pause");
return 0;
}这个问题对于很多初学者来说都不是困难的事情,几个 for 循环就能解决的问题,为什么还要讲一个线段树,直接下课吧。但是,你把这套代码交到洛谷线段树模板这道题上,收获的是满满的TLE。
事情远没有那么简单,在大部分情况下,我们除了需要保证结果的准确,还需要追求速度的提升。那么一些学识广的同学又会说:树状数组处理这种问题不也是很快的吗?的确,线段树与树状数组在同一个复杂量级上(都可以在 $O(\log n)$ 的时间内完成一次操作),树状数组的常数甚至优于线段树,但是树状数组能够完成的操作,线段树也能完成,但是线段树能完成的操作,树状数组不一定能完成。
故,无论如何,学习线段树是非常必要的。
定义
前面说了这么多,也没有介绍线段树的定义。
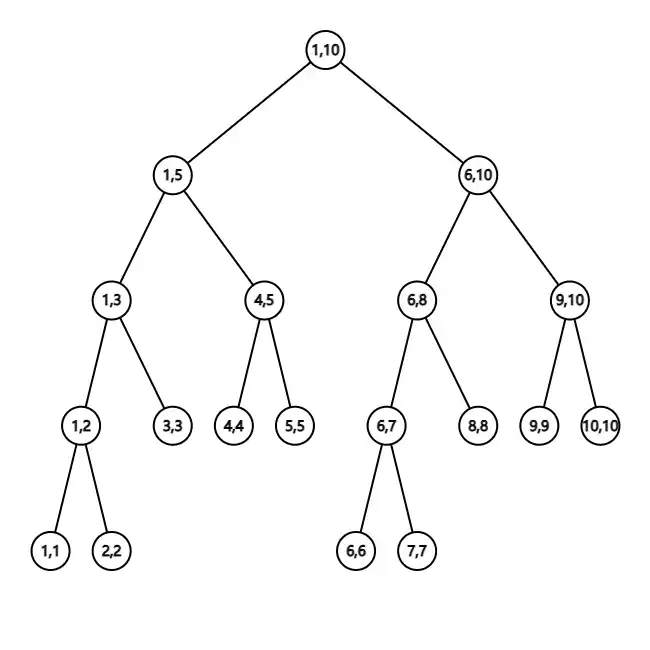
线段树(segment tree)是一种基于分治思想的二叉树,它的每一个节点都对应了一个 $[L,R]$ 区间,叶子节点对应的区间 $L=R$ 。每一个非叶子节点 $[L,R]$ 其左子节点的区间都为 $[L,\frac{(L+R)}{2}]$ ,右子节点的区间都为 $[\frac{(L+R)}{2},R]$ 。这里例子不举多了,一个能够存储 $10$ 个节点的线段树如下图所示。
因为线段树对区间进行二分,是一颗平衡二叉树(平衡二叉树是什么不重要,想要深入了解的话可以看我的博客文章:平衡二叉树),所以树高为 $O(\log n)$ ,树上操作的时间复杂度和树高相关。线段树主要用于更新和查询,一般至少有一个是区间更新或者查询。更新和查询类型的变化多样,灵活运用线段树可以解决多种问题。
限于时间问题,这里只讲解线段树的基本操作,区间查询、单点修改和区间查询、区间修改中求最值以及加和乘两种运算(其余运算类比即可)。
原理:线段树的基本操作
线段树的存储方式
为了更加方便的讲解存储方式,这里以区间最值查询问题来举例。
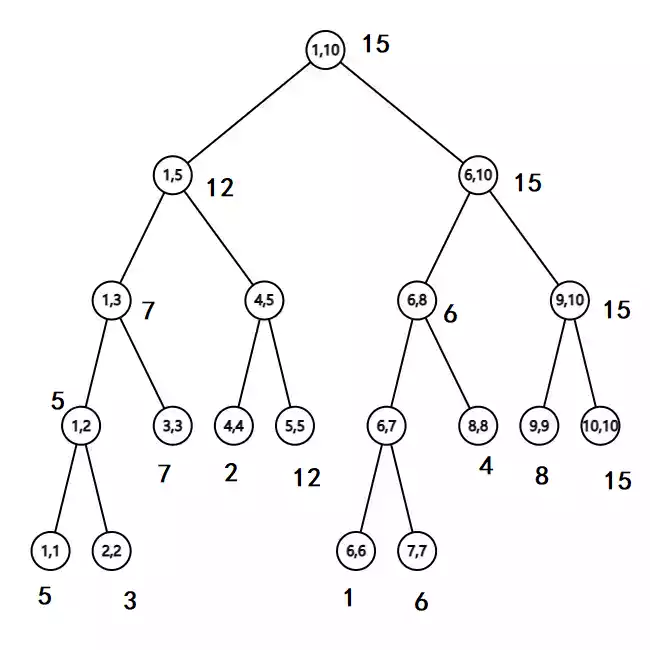
对于区间最值(最大值或者最小值)查询问题,线段树的每个节点都包含三个变量: $l,r,mx$ ,其中 $l$ 和 $r$ 分别表示区间的左右端点, $mx$ 表示 $[l,r]$ 区间的最值。这里以最大值为例(最小值同),按照定义上面的图,给出 $10$ 个元素a[11]={0,5,3,7,2,12,1,6,5,4,8,15},构建的线段树如下图所示:
每一个点的圈内的有序数对表示 $l,r$ ,圈外数字表示该节点表示区间内的最大值,最底层的节点从左到右分别表示a[1] $\sim$ a[10]。
线段树除了最后一层,其他层构成了一颗满二叉树,因此采用顺序存储方式,用一个结构体数组tree[]存储节点。若一个节点的存储下标为 $k$ ,则其左子节点的下标为 $2k$ ,其右子节点的下标为 $2k+1$ 。那么一个节点所存储的三个变量就可以使用tree[k].l、tree[k].r、tree[k].mx表示。、
struct Node
{
long long l,r,mx;
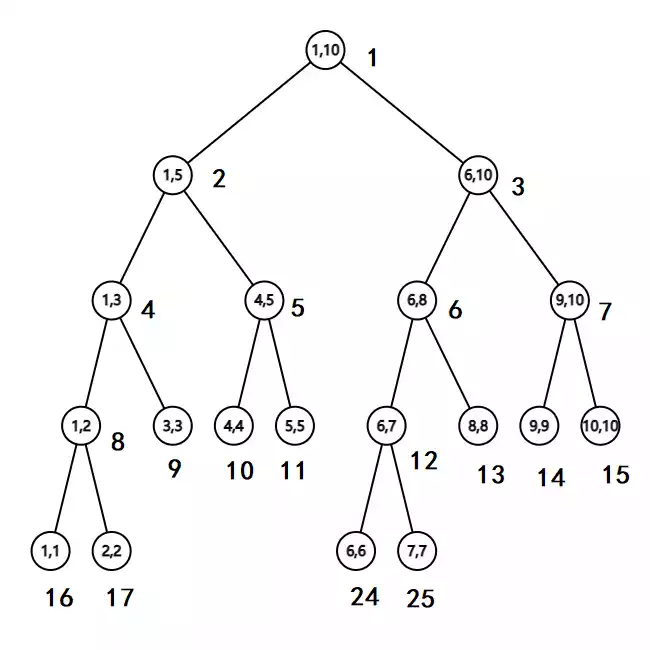
}tree[1000001];线段树根节点的存储下标( $k$ )为 $1$ ,左右子节点根据上述规则编号,最后得到一颗线段树,也就是说线段树内所有有意义的节点并不一定是顺序编号的,例如:
这里圈外的数字表示该节点的下标。
创建线段树
可以采用递归的方法创建一颗线段树,步骤如下:
- 判断是否为叶子节点,根据上述原理可知,叶子节点所存储的数据就是给的数组$\mathbb{a}$中的元素值,那么如果该点的 $l,r$ 值满足 $l=r$ ,那么这个点的最值就是对应位置的元素值。
- 如果不是叶子节点,即 $l\neq r$ 则递归创建左子树和右子树。
- 节点的区间最值等于该节点左右子树的最值的最大值。
void build(int k,int l,int r)//建树:k表示当前节点,l表示当前区间的左端点,r表示当前区间的右端点
{
if(l==r)//当l==r时,表示建树建到了叶子结点,退出递归
{
tree[k].mx=a[l];//a[i]表示原始数据
return;
}
int mid=(l+r)>>1;//位运算,即(l+r)/2
build(k<<1,l,mid);//建立左子树
build(k<<1|1,mid+1,r);//建立右子树
tree[x].mx=max(tree[k<<1].mx,tree[k<<1|1].mx);//更新最值
return;
}单点修改
单点修改指修改一个元素的值,例如将 $a_i$ 修改成 $v$ 。采用递归进行点更新,步骤如下:
- 如果是叶子节点, $l=r=i$ ,则修改该节点的最值为 $v$。
- 如果是非叶子节点,则判断是在左子树中还是右子树中更新。
- 返回时更新节点的最值。
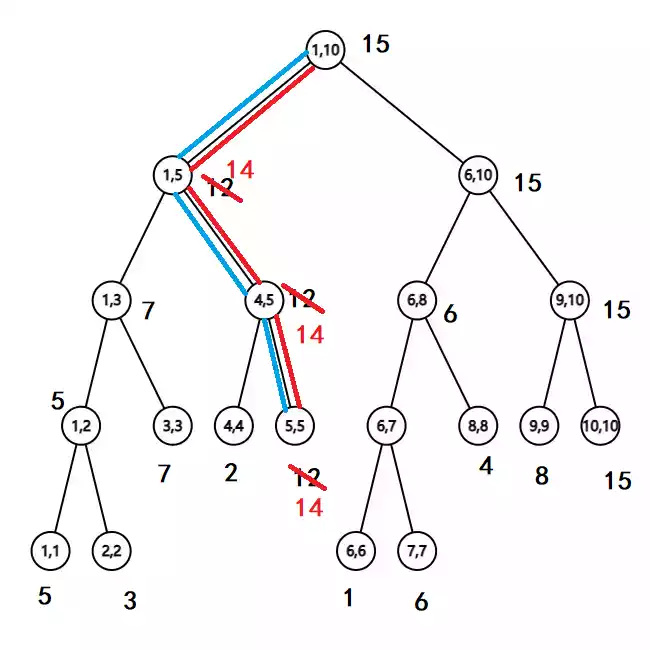
例如,修改第五个节点的值为 $14$ 时,先从树根向下找第 $5$ 个元素所在的叶子节点,将其值改为 $14$ ,返回时更新路径上所有节点的最值。
图中蓝线表示递推过程,红线表示回溯过程及其操作,下同。
void add(int k,int i,int v)//单点修改:k表示当前节点,i表示当前要修改的数据的位置,y表示要修改多少的值
{
if(tree[k].l==tree[k].r)//找到了叶子结点,即i点,退出递归
{
tree[k].mx=v;//这里的=可以换成其他运算符
return;
}
int mid=(tree[k].l+tree[k].r)>>1;
if(i<=mid)//若要找的点在自己的左儿子表示的区间中
add(k<<1,tree[k].l,mid,i,v);
if(i>mid)//若要找的点在自己的右儿子表示的区间中
add(k<<1|1,mid+1,tree[k].r,i,v);
tree[k].mx=max(tree[k<<1].mx,tree[k<<1|1].mx);//更新节点
}区间查询
区间查询指查询一个 $[l,r]$ 区间的最值。采用递归的方法进行区间查询,步骤如下:
- 若节点所在的区间被查询区间 $[l,r]$ 覆盖,则返回该节点的最值。
- 判断是在左子树中查询还是在右子树中查询。
- 返回最最值。
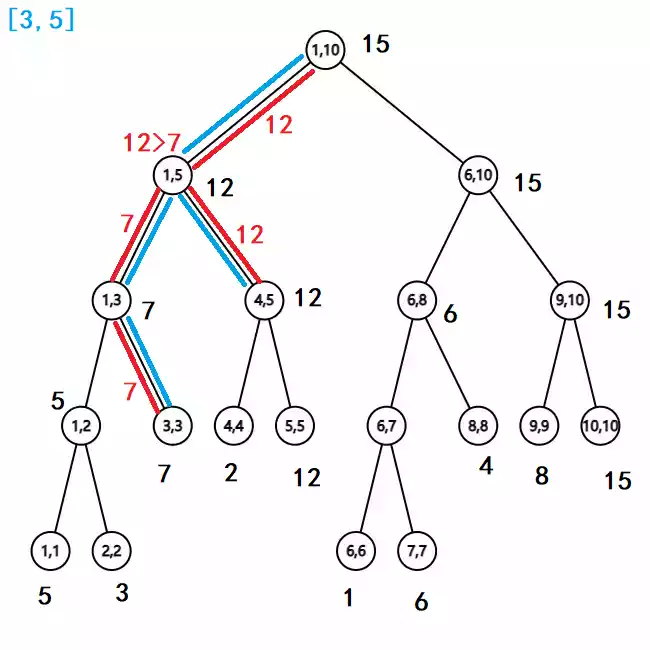
例如,在原图中查询 $[3,5]$ 的最值,过程如图:
int ask(int k,int l,int r)//单点查询:k表示当前节点l表示要查询的区间的左端点,r表示要查询的区间的右端点。
{
if(l<=tree[k].l&&tree[k].r<=r)//如果当前区间完全包括在要查询的区间的范围内,返回节点的值
return tree[k].mx;
int mid=(tree[k].l+tree[k].r)>>1;
int res=0;
if(l<=mid)//查询左儿子
res=max(ask(k<<1,l,r),res);
if(r>mid)//查询右儿子
res=max(ask(k<<1|1,l,r),res);
return res;//返回最值
}段落小结
至此,你已经学会了构建线段树、单点修改、区间查询的操作,虽然是以最大值为例讲解,但是将其更换为其他运算操作依旧成立。
但是线段树更加强大之处在于它可以实现区间修改和区间查询。但是连续使用单点修改的方法进行区间修改的时间复杂度较高,所以我们需要一个懒惰标记,下面讲解懒惰标记的使用
原理:懒惰标记与区间操作
懒惰标记
懒惰标记是什么?本区间已经被更新过了,但是子区间却没有被更新过,懒惰标记记录下来被更新的信息是什么。
你可能还是不懂,但是在后面的实例讲解中,你会有更加深刻地理解。
区间更新
对 $[l,r]$ 区间进行更新,例如将 $[l,r]$ 区间的所有元素都更新成 $v$ ,步骤如下:
- 若当前节点的区间被 $[l,r]$ 完全覆盖,则仅对该节点进行更新并做好懒惰标记,表示该节点已经被更新,对该节点的子节点暂时不更新,我们可以在查询的时候根据懒惰标记再向下更新(减少了一些不必要的操作,大幅减小复杂度)。
- 判断是在左子树中更新还是在右子树中更新。在更新过程中,可能会碰到带有懒惰标记的节点,那么就将该点的懒惰标记传给子节点,并清除当前节点的懒惰标记。
- 在返回时更新最值。
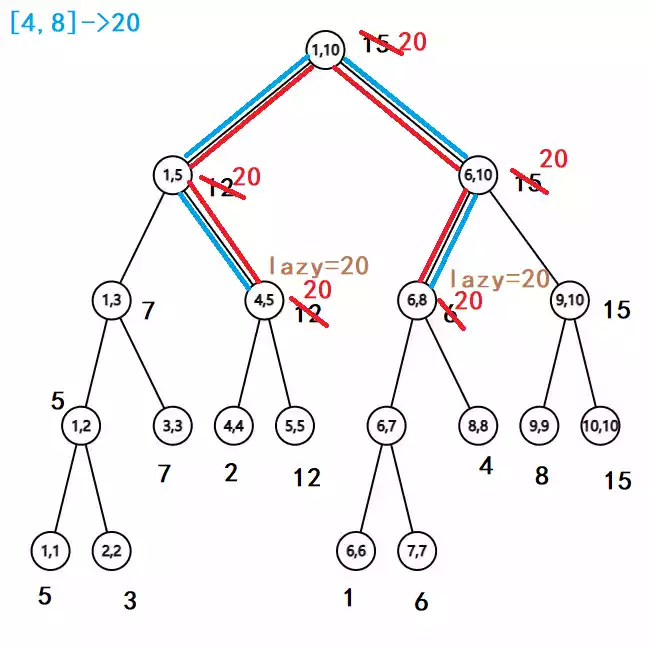
例如,在 $[1,10]$ 区间的线段树中修改 $[4,8]$ 区间的值为 $20$ ,过程如下:
void pushdown(long long k)//懒惰标记下推:k表示懒惰标记所在节点
{
if(tree[k].lz!=0)//判断是否有懒惰标记
{
tree[k<<1].lz=tree[k].lz;//将懒惰标记传递给左右儿子
tree[k<<1|1].lz=tree[k].lz;
long long mid=(tree[k].l+tree[k].r)>>1;
tree[k<<1].mx=tree[k].lz;//修改当前节点的值
tree[k<<1|1].mx=tree[k].lz;
tree[k].lz=0;//清空标记
}
return;
}
void update(long long k,long long l,long long r,long long v)//区间修改,k表示当前修改的节点编号,l表示要修改的区间左端点,r表示要修改的区间右端点,v表示将[l,r]区间内的值改为v
{
if(tree[k].l>=l&&tree[k].r<=r)
{
tree[k].mx=v;//将要修改的值乘区间元素个数于原数相加得到当前值
tree[k].lz=v;//标记懒惰标记
return;
}
pushdown(k);//懒惰标记下移
long long mid=(tree[k].l+tree[k].r)>>1;
if(l<=mid)
update(k<<1,l,r,v);
if(r>mid)
update(k<<1|1,l,r,v);
tree[k].sum=(tree[k<<1].mx,tree[k<<1|1].mx);
return;
}这时候懒惰标记还没有发挥作用,不要急,看一下区间查询。
区间查询
带懒惰标记的区间查询和普通的区间查询有所不同,在查询中如果遇到节点有懒惰标记的节点就下传懒惰标记,相当于在查询的时候顺便更新了节点。
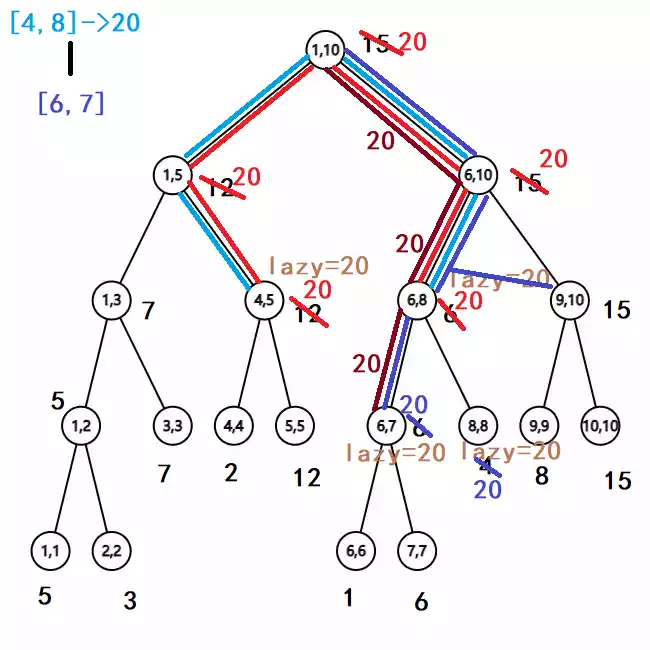
以上图为例,查询 $[6,7]$ 区间的最值,过程如下:
深蓝色表示查询操作的递推及其操作,深红色表示回溯结果。
long long search(long long k,long long l,long long r)//区间查询
{
if(tree[k].l>=l&&tree[k].r<=r)
return tree[k].mx;
pushdown(k);//查询是将懒惰标记下移
long long s=0;
long long mid=(tree[k].l+tree[k].r)>>1;
if(l<=mid)
s=max(s,search(k<<1,l,r));
if(r>mid)
s=max(s,search(k<<1|1,l,r));
return s;
}段落小结
至此,线段树的部分简单操作已经教学完成,灵活运用懒惰标记是很重要的,分清什么时候需要下传标记就可以轻松完成程序。
训练:
入门级
稍微一变通就可以过
新手级
你需要思考懒惰标记的应该如何下传
提高级
你需要思考懒惰标记的计算顺序
你觉得你很可以级
这两个可能需要更多的知识辅助,可以尝试。
总结
本讲义以求最值为模板,以四则运算为练习,举一反三,希望同学们课后加强练习。
这只是线段树最基础部分,还有其他线段树的延伸,有兴趣的同学可以了解一下。
答案链接线段树页面后部分,这是我以前写的博客,如果这篇博客看不太懂的话,可以试试我过去写的,两篇思路不同。