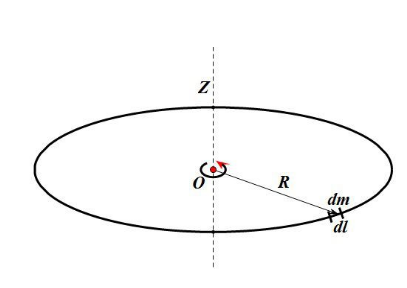
1. 转轴通过圆环中心与环面垂直的转动惯量

$$I=m{R}^2$$
推导：
在圆环上取一质元，其质量为 $dm=\lambda dl$，其中 $\lambda =\frac{m}{2\pi R}$ 为线密度，$dl$ 为圆弧元。质元对转轴的元转动惯量为：
$$dI=R^{2}dm=\lambda R^{2}dl$$
对整个圆环积分：

$$I={\int }_0^{2\pi R}\lambda R^{2}dl=\lambda R^2\cdot 2\pi R=2\pi \lambda R^3$$

代入 $\lambda =\frac{m}{2\pi R}$，得：

$$I=2\pi \cdot \frac{m}{2\pi R}\cdot R^3=m{R}^2$$

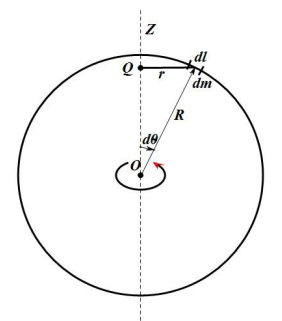
2. 转轴沿圆环直径的转动惯量

$$I=\frac{m{R}^2}{2}$$
推导：
质元质量 $dm=\frac{m}{2\pi }d\theta$（$\theta$ 为质元与转轴的夹角）。质元的转动惯量元为：

$$dI=(R\sin \theta {)}^{2}dm=\frac{m{R}^2}{2\pi }{\sin }^2\theta d\theta$$

利用三角恒等式 ${\sin }^2\theta =\frac{1-\cos 2\theta }{2}$，积分得：

$$I=\frac{m{R}^2}{2\pi }{\int }_0^{2\pi }\frac{1-\cos 2\theta }{2}d\theta =\frac{m{R}^2}{4\pi }[{\int }_0^{2\pi }d\theta -{\int }_0^{2\pi }\cos 2\theta d\theta ]$$

第二项积分 ${\int }_0^{2\pi }\cos 2\theta d\theta =0$，故：

$$I=\frac{m{R}^2}{4\pi }\cdot 2\pi =\frac{m{R}^2}{2}$$

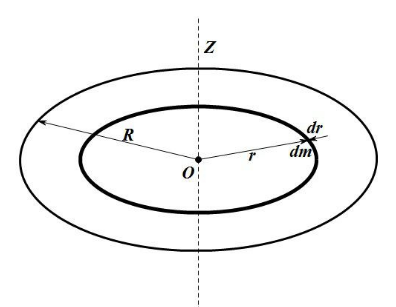
3. 转轴通过薄圆盘中心与圆盘垂直的转动惯量

$$I=\frac{m{R}^2}{2}$$
推导：
取半径为 $r$、宽度 $dr$ 的细圆环，质量 $dm=2\pi r\sigma dr$（面密度 $\sigma =\frac{m}{\pi R^2}$）。转动惯量元为：

$$dI=r^{2}dm=2\pi \sigma r^{3}dr$$

积分得：

$$I={\int }_0^{R}2\pi \sigma r^{3}dr=2\pi \sigma \cdot \frac{R^4}{4}=\frac{\pi \sigma R^4}{2}$$

代入 $\sigma =\frac{m}{\pi R^2}$，得：

$$I=\frac{\pi \cdot \frac{m}{\pi R^2}\cdot R^4}{2}=\frac{m{R}^2}{2}$$

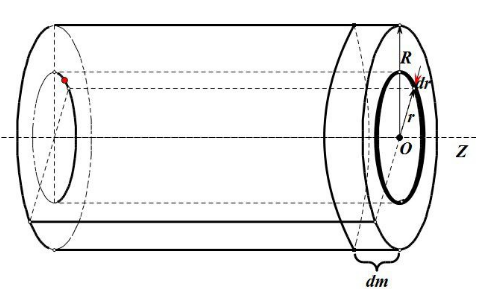
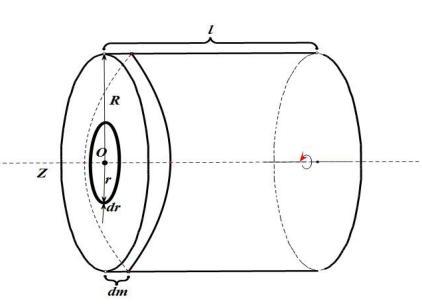
4. 转轴沿圆筒几何轴的转动惯量

$$I=\frac{m}{2}(R^2+r^2)$$
推导：
将圆筒视为由无数同心圆环组成。取半径 $r$ 的元圆筒，质量 $dm=2\pi \sigma rdr$，转动惯量元为：

$$dI=r^{2}dm=2\pi \sigma r^{3}dr$$

总转动惯量为内外半径积分之差：

$$I={\int }_r^{R}2\pi \sigma r^{3}dr=\frac{\pi \sigma }{2}(R^4-r^4)$$

因 $\sigma =\frac{m}{\pi (R^2-r^2)}$，代入得：

$$I=\frac{\pi \cdot \frac{m}{\pi (R^2-r^2)}}{2}(R^4-r^4)=\frac{m(R^2+r^2)}{2}$$

5. 转轴沿圆柱体几何轴的转动惯量

$$I=\frac{m{R}^2}{2}$$
推导：
将圆柱体分解为无数薄圆盘。取厚度为 $dy$ 的微圆盘，质量 $dm=\sigma \pi R^{2}dy$（$\sigma$ 为体密度）。薄圆盘的转动惯量元为：

$$dI=\frac{1}{2}{R}^{2}dm=\frac{1}{2}{R}^2\cdot \sigma \pi R^{2}dy$$

总转动惯量为：

$$I={\int }_0^L\frac{\sigma \pi R^4}{2}dy=\frac{\sigma \pi R^{4}L}{2}$$

因总质量 $m=\sigma \pi R^{2}L$，代入得：

$$I=\frac{m{R}^2}{2}$$

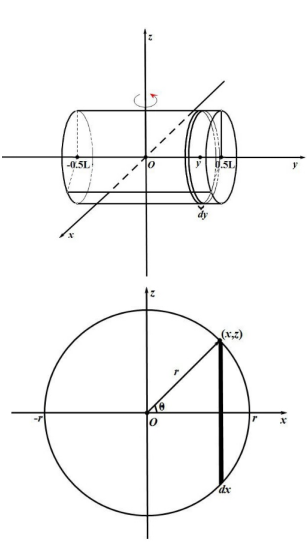
6. 转轴通过圆柱体中心与几何轴垂直的转动惯量

$$I=\frac{m{r}^2}{4}+\frac{m{L}^2}{12}$$
推导：
取微细长方体，坐标 $(x,y)$，质量元 $dm=\rho \cdot 2z\cdot dxdy$（$z=r\sin \theta$）。转动惯量元为：

$$dI=(x^2+y^2)dm=\rho \cdot 2r\sin \theta \cdot (x^2+y^2)dxdy$$

转换为极坐标：$x=r\cos \theta$，积分得：

$$I=\rho {\int }_{-L/2}^{L/2}{\int }_0^{2\pi }{r}^3\sin \theta ({\cos }^2\theta +y^2)d\theta dy$$

分离积分并计算，最终结果为：

$$I=\frac{m{r}^2}{4}+\frac{m{L}^2}{12}$$

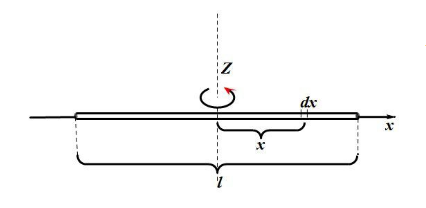
7. 转轴通过细棒中心与棒垂直的转动惯量

$$I=\frac{m{l}^2}{12}$$
推导：
取质元 $dm=\lambda dx$（线密度 $\lambda =\frac{m}{l}$），距转轴距离为 $x$。转动惯量元为：

$$dI=x^{2}dm=\lambda x^{2}dx$$

积分区间为 $-l/2$ 到 $l/2$：

$$I=\lambda {\int }_{-l/2}^{l/2}{x}^{2}dx=\lambda {\left[\frac{x^3}{3}\right]}_{-l/2}^{l/2}=\frac{\lambda l^3}{12}$$

代入 $\lambda =\frac{m}{l}$，得：

$$I=\frac{m{l}^2}{12}$$

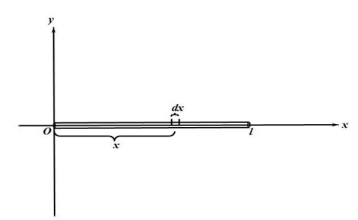
8. 转轴通过细棒端点与棒垂直的转动惯量

$$I=\frac{m{l}^2}{3}$$
推导：
积分区间改为 $0$ 到 $l$，转动惯量元相同：

$$I=\lambda {\int }_0^l{x}^{2}dx=\lambda {\left[\frac{x^3}{3}\right]}_0^l=\frac{\lambda l^3}{3}$$

代入 $\lambda =\frac{m}{l}$，得：

$$I=\frac{m{l}^2}{3}$$

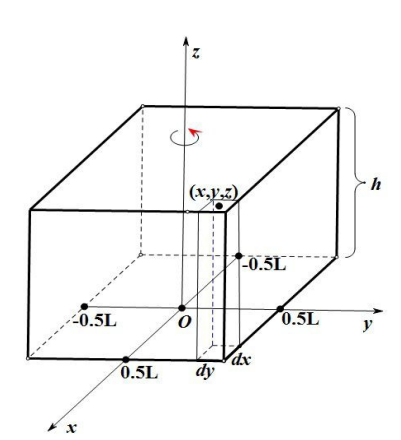
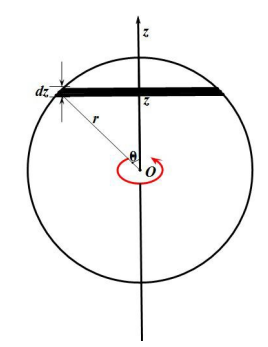
9. 转轴通过球体沿直径的转动惯量

$$I=\frac{2m{r}^2}{5}$$
推导：
将球体分解为薄圆盘。取距球心 $z$ 处厚度 $dz$ 的圆盘，半径 $R_g=\sqrt{r^2-z^2}$，质量 $dm=\rho \pi R_g^{2}dz$。圆盘转动惯量元为：

$$dI=\frac{1}{2}{R}_g^{2}dm=\frac{\rho \pi }{2}(r^2-z^2{)}^{2}dz$$

总转动惯量为：

$$I=\frac{\rho \pi }{2}{\int }_{-r}^r(r^2-z^2{)}^{2}dz$$

展开积分并计算，结合总质量 $m=\frac{4}{3}\pi \rho r^3$，得：

$$I=\frac{2m{r}^2}{5}$$

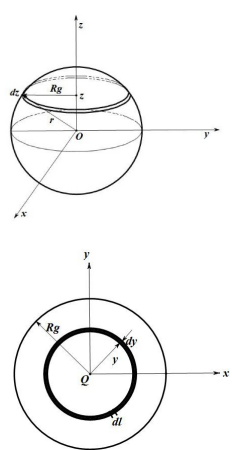
10. 转轴沿球壳直径的转动惯量

$$I=\frac{2m{r}^2}{3}$$
推导：
取圆心角 $d\theta$ 的圆环，半径 $R_g=r\sin \theta$，质量元 $dm=\sigma \cdot 2\pi r\sin \theta \cdot rd\theta$（面密度 $\sigma =\frac{m}{4\pi r^2}$）。转动惯量元为：

$$dI=R_g^{2}dm=2\pi \sigma r^4{\sin }^3\theta d\theta$$

积分得：

$$I=2\pi \sigma r^4{\int }_0^{\pi }{\sin }^3\theta d\theta =\frac{8\pi \sigma r^4}{3}$$

代入 $\sigma =\frac{m}{4\pi r^2}$，得：

$$I=\frac{2m{r}^2}{3}$$

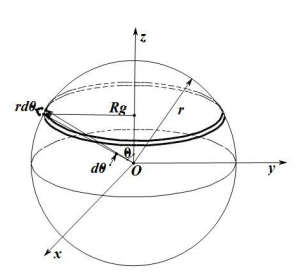
11. 转轴沿底面是正方形的长方体的几何轴的转动惯量

$$I=\frac{m{L}^2}{6}$$
推导：
取微元 $dm=\rho hdxdy$，转动半径 $r=\sqrt{x^2+y^2}$。转动惯量元为：

$$dI=(x^2+y^2)dm=\rho h(x^2+y^2)dxdy$$

在 $[-L/2,L/2]\times [-L/2,L/2]$ 区域积分：

$$I=\rho h{\int }_{-L/2}^{L/2}{\int }_{-L/2}^{L/2}(x^2+y^2)dxdy=\rho h\cdot \frac{L^4}{6}$$

代入总质量 $m=\rho h{L}^2$，得：

$$I=\frac{m{L}^2}{6}$$

12. 转轴沿圆盘直径的转动惯量

$$I=\frac{m{r}^2}{4}$$
推导：
取宽度 $dz$ 的长条，长度 $2\sqrt{r^2-z^2}$，质量元 $dm=\sigma \cdot 2\sqrt{r^2-z^2}dz$。转动惯量元为：

$$dI={\int }_{-R_g}^{R_g}{x}^2\cdot \sigma dxdz=\frac{4\sigma }{3}(r^2-z^2{)}^{3/2}dz$$

总转动惯量：

$$I=\frac{4\sigma }{3}{\int }_{-r}^r(r^2-z^2{)}^{3/2}dz=\frac{\sigma \pi r^4}{4}$$

代入 $\sigma =\frac{m}{\pi r^2}$，得：

$$I=\frac{m{r}^2}{4}$$