一、平移坐标轴所致的坐标变换公式

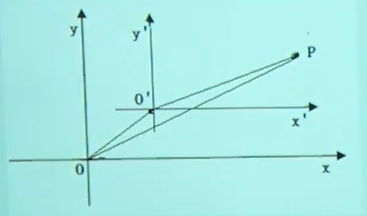
设$O$是平面上的一个点，以它为原点，如图构建直角坐标系$xOy$。设$O'$是平面上的一点，其坐标是$O^{\prime}(x_0,y_0)$.平移直角坐标系$xOy$使得新的原点为$O'$.记平移后的坐标系的两个数轴分别为$x'$和$y'$、坐标系为$x'O'y'$对于平面上的任意一点$P$，如果它在$xOy$和$x'Oy'$中的坐标分别是$(x,y)$和$( x^\prime , y^\prime )$，由于在坐标系$xOy$中
$$\overrightarrow{OO^{\prime}}=(x_0,y_0),\:\overrightarrow{O^{\prime}P}=(x^{\prime},y^{\prime}),\overrightarrow{OP}=(x,y)$$
$$\overrightarrow{OP}=\overrightarrow{OO^{\prime}}+\overrightarrow{O^{\prime}P}$$

由此得到坐标平移公式：$$\begin{cases}x=x'+x_0 ,\\[2ex]y=y'+y_0\end{cases}$$

例1 试判断二次曲线的$y^2-2x+4y+8=0$的类型

解 配方化二次曲线方程为
$$(y+2)^2=2(x-2)$$
令
$$\begin{cases}x'=x-2\\y'=y+2\end{cases}\quad\text{即}\quad\begin{cases}x=x'+2\\y=y'-2\end{cases}$$
则二次曲线在以$(2,-2)$为原点的坐标系中的方程为
$$y^{\prime2}=2x^{\prime}$$
所以，该二次曲线是一条顶点在$(2,-2)$、开口向右的抛物线。

二、旋转坐标轴所致的坐标变换公式

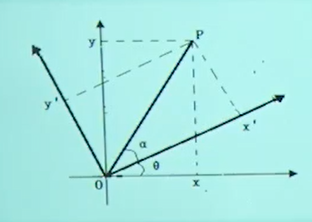
设$O$是平面上确定的点，以它为原点分别构建直角坐标系$xOy$和$x'Oy'$.如图所示，在这两个坐标系中，$x$轴和$x'$轴的正向夹角为$\theta$，单位长度一致。直角坐标系$x'Oy'$可以看成为由直角坐标系$xOy$旋转$\theta$角度所得如果$\theta$描述的是$x$轴经逆时针旋转到$x'$轴时所划过的角度，则$\theta$ 取正号，否则取负号，对于平面上的任意一点$P$, 如果它在$xOy$和$x'Oy'$中的坐标分别是$(x,y)$和$(x^\prime,y^\prime)$，这两个坐标之间存在如下关系：

首先，点$P$在这两个坐标系中的坐标分别为$\begin{cases}x=\mid OP\mid\cos(\alpha+\theta)\\y=\mid OP\mid\sin(\alpha+\theta)\end{cases}\begin{cases}x^{\prime}=\mid OP\mid\cos\alpha\\y^{\prime}=\mid OP\mid\sin\alpha\end{cases}$

依三角函数的和差化积公式，得：
$$\begin{cases}x=\mid OP\mid\cos(\alpha+\theta)=\mid OP\mid\cos\alpha\cos\theta-\mid OP\mid\sin\alpha\sin\theta\\y=\mid OP\mid\sin(\alpha+\theta)=\mid OP\mid\sin\alpha\cos\theta+\mid OP\mid\cos\alpha\sin\theta\end{cases}$$

最终得到坐标旋转公式：$\begin{cases} x= x^{\prime }\cos \theta - y^{\prime }\sin \theta \\ y= x^{\prime }\sin \theta + y^{\prime }\cos \theta & \end{cases}$

在以后得线性代数课程中，会进一步来解释旋转坐标问题。

如果我们将$xOy$视为旧坐标系，将$x'Oy'$视为新坐标系，那么，上式的坐标变换公式是用点在新坐标系中的坐标来表示点在旧坐标系中的坐标。

三、圆锥曲线的标准化

我们只有将含有非零系数$xy$项曲线方程改造成为二次曲线的标准方程，才可以判断出二次曲线的类型。

例2 试判断二次曲线的$x^2-2xy+y^2=2\sqrt{2}(x+y)$的类型。

解 我们首先将坐标旋转公式$\begin{cases}x=x^{\prime}\cos\theta-y^{\prime}\sin\theta\\y=x^{\prime}\sin\theta+y^{\prime}\cos\theta\end{cases}$代入所给方程中，得：
$$\begin{aligned}\left(\cos\theta-\sin\theta\right)^2x^{\prime2}+\left(\cos\theta+\sin\theta\right)^2y^{\prime2}-2\left(\cos\theta-\sin\theta\right)\left(\cos\theta+\sin\theta\right)x^{\prime}y^{\prime}\\=2\sqrt{2}\left(\cos\theta+\sin\theta\right)x^{\prime}+2\sqrt{2}\left(\cos\theta-\sin\theta\right)y^{\prime}\end{aligned}$$
其次，令上式中含项$x^{\prime}y^{\prime}$的系数为零，即令：
$$2\bigl(\cos\theta-\sin\theta\bigr)\bigl(\cos\theta+\sin\theta\bigr)=0$$
所给方程在坐标变换$\begin{cases}x=\frac{\sqrt{2}}{2}\left(x^{\prime}-y^{\prime}\right)\\y=\frac{\sqrt{2}}{2}\left(x^{\prime}+y^{\prime}\right)\end{cases}$下化为 $y\prime ^2=2x^{\prime}$
得$\theta=\frac\pi4$，故所给的二次曲线是新坐标系中的开口朝右、顶点在原点的抛物线。换句话说，所给的二次曲线方程是一条以原点为顶点、以直线y=x为对称轴且开口朝右上角的抛物线。