一、反三角函数定义

1、反正弦函数

由于正弦函数的单调区间为$[ - \frac \pi 2+ 2k\pi , \frac \pi 2+ 2k\pi ]$ 和 $[ \frac \pi 2+ 2k\pi , \frac {3\pi }2+ 2k\pi ],k\in \mathbb{Z}$在每个单调区间上正弦函数都有反函数。例如在以下区间中，存在：

$y=\sin x,x\in[-\frac\pi2,\frac\pi2]$
对于任意的 $y\in[-1,1]$，都存在唯一的$x\in [ - \frac \pi 2, \frac \pi 2] $，使得 $\sin x=y$.
因此正弦函数在该闭区间上的反函数存在，记为$x=\arcsin y,(-1\leq y\leq1)$

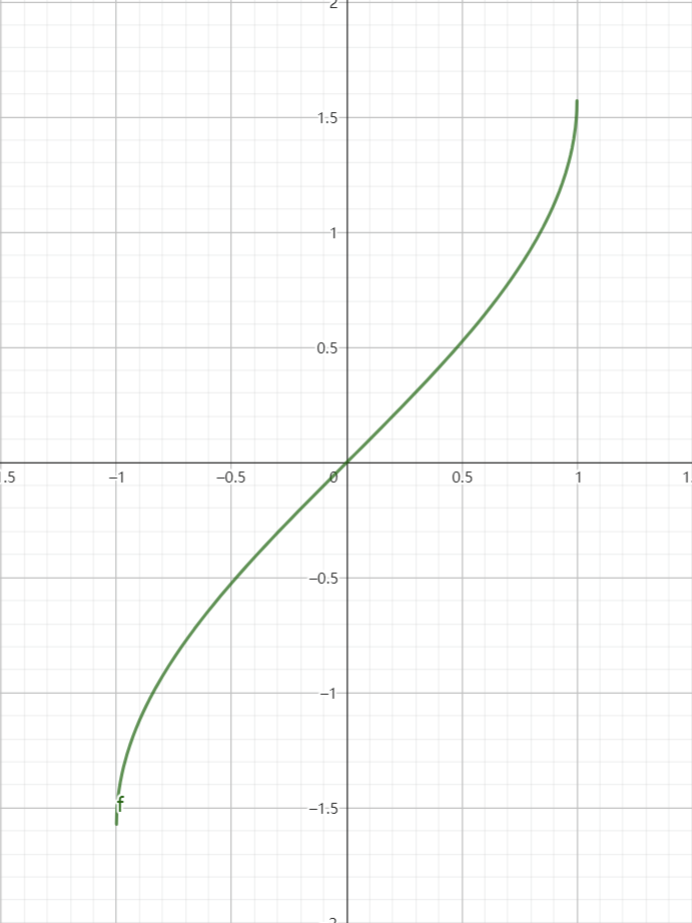
由于符号的习惯，我们通常用$x$表示自变量，这样正弦函数在$[-\frac\pi2,\frac\pi2]$上的反函数为
$$y=\arcsin x(-1\leq x\leq1)$$

限定在$\left [ - \frac \pi 2+ 2k\pi , \frac \pi 2+ 2k\pi \right ]$上研究正弦函数的反函数。
对于任意的$y\in [ - 1, 1]$, $\arcsin y+ 2k\pi \in [ - \frac \pi 2+ 2k\pi , \frac \pi 2+ 2k\pi ]$以及$\sin(\arcsin y+2k\pi)=\sin(\arcsin y)=y$.
因此$x=\arcsin y+2k\pi$是正弦函数在$[-\frac\pi2+2k\pi,\frac\pi2+2k\pi]$上的反函数。

限定在$[\frac\pi2+2k\pi,\frac{3\pi}2+2k\pi]$上研究正弦函数的反函数。
对于任意的$y\in[-1,1],(\pi-\arcsin y)+2k\pi\in[\frac\pi2+2k\pi,\frac{3\pi}2+2k\pi]$以及$\sin((\pi-\arcsin y)+2k\pi)=\sin(\pi-\arcsin y)=y$,
因此 $x= ( \pi - \arcsin y) + 2k\pi$是正弦函数在$[\frac\pi2+2k\pi,\frac{3\pi}2+2k\pi]$上的反函数。

2、反余弦函数

由于余弦函数的单调区间为$[2k\pi,(2k+1)\pi]$和$[(2k-1)π,2kπ],k\in\mathbb{Z}$，在每个单调区间上余弦函数都有反函数。

限定在区间$[0,\pi]$上研究余弦函数$y=\cos x$.
对于任意的$y\in[-1,1]$，都存在唯一的 $x\in [ 0, \pi ]$，使得$\cos x=y$.
因此余弦函数在该闭区间上的反函数存在，记为$x=\arccos y(-1\leq y\leq1)$

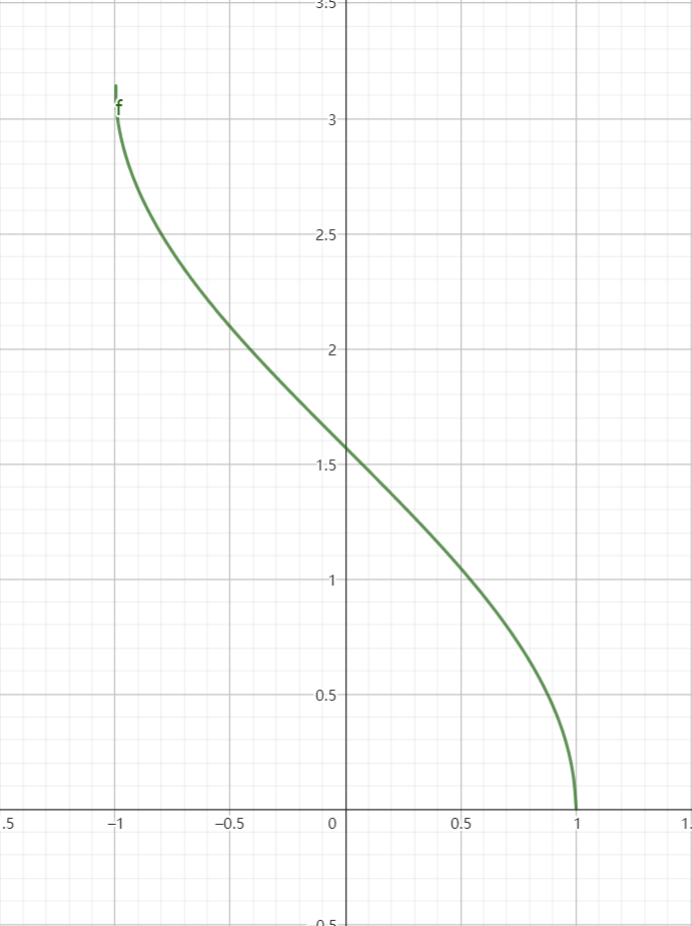
由于符号的习惯，我们通常用$x$表示自变量，这样余弦函数在$[0,\pi]$上的反函数为
$$y=\arccos x(-1\leq x\leq1)$$

3、反正切函数

由于正切函数的单调区间为 $\left ( - \frac \pi 2+ k\pi , \frac \pi 2+ k\pi \right ) k\in \mathbb{Z}$在每个单调区间上正切函数都有反函数。

限定在区间$\left(-\frac\pi2,\frac\pi2\right)$上研究正切函数$y=\tan x$.
对于任意的 $y\in\mathbb{R}$, 都存在唯一的$x\in \left ( - \frac \pi 2, \frac \pi 2\right )$, 使得 $\tan x= y$.
因此正切函数在该区间上的反函数存在，记为$x=\arctan y(y\in\mathbb{R})$

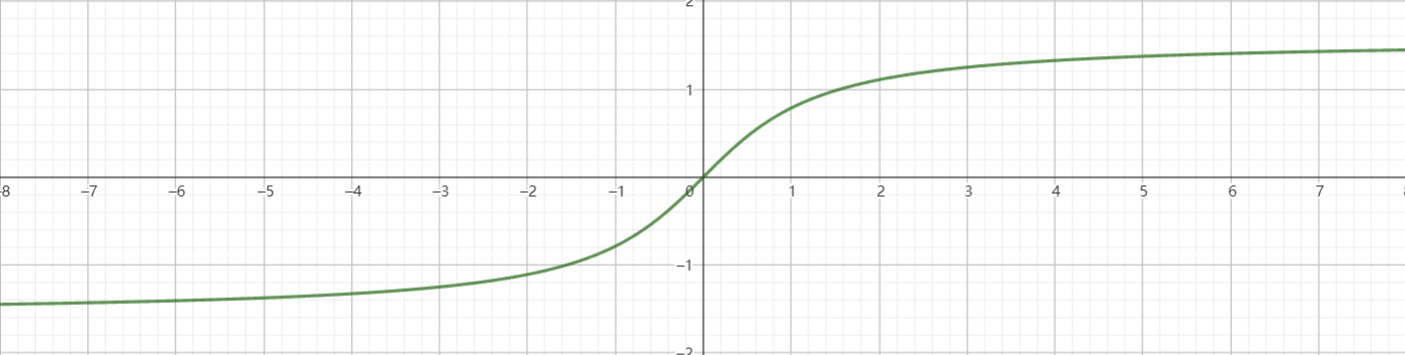
由于符号的习惯，我们通常用$x$表示自变量，这样正切函数在$(-\frac\pi2,\frac\pi2)$上的反函数为
$$y=\arctan x,x\in\mathbb{R}$$

二、反三角函数的计算

例1 例1 求函数$y=\frac1{\arcsin\sqrt{x}}$的定义域和值域。

解 定义域为$0<x\leq1$.由于反正弦函数的递增性，可得$0=\arcsin0<\arcsin x\leq\arcsin1=\frac\pi2$
由此值域为$[\frac2\pi,+\infty)$.

例2 求$\cos ( 2\arccos \frac 14- \arccos \frac 15)$的值。
解 设$A= \arccos \frac 14, B= \arccos \frac 15$，由此有$\cos A= \frac 14, \cos B= \frac 15, \sin A= \frac {\sqrt {15}}4, \sin B= \frac {2\sqrt {6}}5$
于是：
$$\begin{aligned}原式 &=\cos(2A-B)\\&=\cos2A\cos B+\sin2A\sin B \\ &=(2\cos^{2}A-1)\cos B+2\sin A\cos A\sin B\\&=-\frac{7}{8}\cdot\frac{1}{5}+2\frac{\sqrt{15}}{4}\cdot\frac{1}{4}\cdot\frac{2\sqrt{6}}{5}\\&=\frac{6\sqrt{10}-7}{40}\end{aligned}$$

例3 设$0\leq x\leq1$，求 $2 \arcsin x+\arccos(2x^2-1)$的值。

解 令$x=\cos\alpha,0\leq\alpha\leq\frac{\pi}{2}$，则：
$$\begin{aligned}&2\arcsin x+\arccos(2x^2-1)\\=&2\arcsin(\cos\alpha)+\arccos(2(\cos\alpha)^2-1)\\=&2\arcsin(\sin(\frac\pi2-\alpha))+\arccos(\cos2\alpha)\\=&2(\frac{\pi}{2}-\alpha)+2\alpha\\=&\pi\end{aligned}$$

关注含$x$的表达式的值域与反三角函数的定义域！