一、复数的定义及各种表达形式

1、代数定义

1. 如果量$z$能写成如下形式：
   $$z=a+b \mathrm{i} ,a,b\in R,$$
   则称$z$ 是一个复数。这里$\mathrm{i}$是一个符号，称作虚数单位。实数$a,b$分别称作复数$z$的实数部分（或简称实部）和虚数部分（或简称虚部），记为：
   $$\mathrm{Re}\left(z\right)=a,\mathrm{Im}\left(z\right)=b$$
2. 复数的全体所组成的集合记为
   $$\mathbb{C}=\left\{a+bi\mid a,b\in R\right\}.$$
3. 实数是虚部为零的复数。
   当$\mathrm{Re}\left(z\right)=0$时，复数$z$简记为$z=b\mathrm{i}$.此时，称
   复数$z$为纯虚数
   当$\mathrm{Im}\left(z\right)=0$时，复数$z$简记为$z=a$.
   当$\mathrm{Im}\left(z\right)=1$时，复数$z$简记为$z=a+\mathrm{i}$.
   简记实部和虚部均为零的复数为$0$.
4. 依据约定，我们有 $\mathbb{R} \subsetneqq \mathbb{C}$.
   对于任意的两个复数$z_1,z_2$,当且仅当$\mathrm{Re}(z_1)=\mathrm{Re}(z_2)$且$\mathrm{Im}(z_1)=\mathrm{Im}\left(z_{2}\right)$时，我们称$z_1$与$z_2$相等，记为$z_1=z_2$.
5. 依据约定，我们有：
   $$\mathrm{i}=1\mathrm{i}$$
   $$a=a+0\mathrm{i},a\in \mathbb{R}$$

2、几何意义

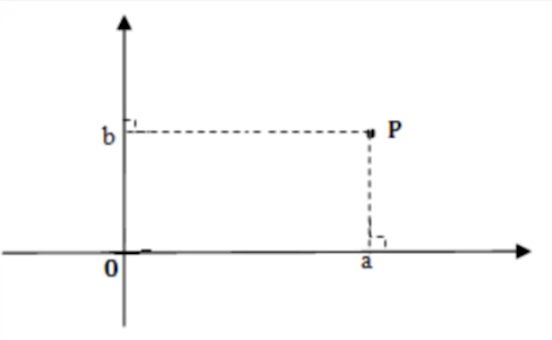
取平面上的一点作为参照点并记为$O$,过点$O$作相互垂直的两条实数轴，两条数轴都以$O$作为原点， 并具有相同的单位长度。习惯上，我们总是让其中的一条数轴的正向向右，另一条数轴的正向朝上，即构建了一个平面笛卡尔坐标系。

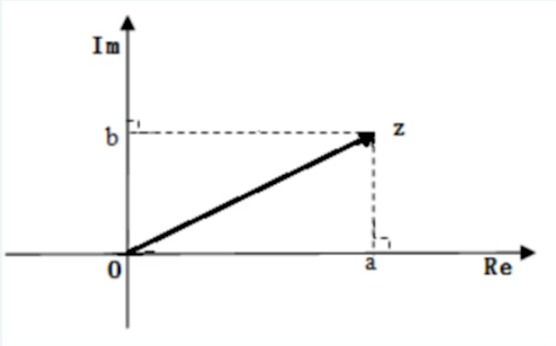
已知复数$z=a+b\mathrm{i}$,这里$a,b\in\mathbb{R}$，如图构造$z$，在平面上的唯一对应点$P$，这里点$P$在由点$O$及横竖两数轴所构成的平面坐标系中的坐标为$(a,b)$.

反之，若已知平面上的点$P$，它在在由$O$及横竖两数轴所构成的平面坐标系中的坐标为$(a,b)$，则存在唯一的复数$z$满足$z=a+b\mathrm{i}$.据此，我们不难获知，复数与上述平面上的点——对应。习惯上，我们称这样的平面为复（数）平面。称水平数轴为实轴，称竖向数轴为虚轴，记为$\mathrm{Re,Im}$. 我们常将复平面上与给定复数$z$对应的点$P$直接标注为$z$ 由于平面坐标系中的点与向径是一一对应的，因此，复平面上的复数也就与向径（有向线段$\overrightarrow{Oz}$）一一对应。

以后，复数、复平面上与之对应的点及向径为同一体，不做区分。

3、三角函数表达形式

1. 已知复数$z=a+b\mathrm{i}$,这里$a , b\in \mathbb{R}，$ $z$ 的模长：有向线段$\overrightarrow{Oz}$ 的长度，记作$|z|$.

$$|z|=\sqrt{a^2+b^2}=\sqrt{\mathrm{Re}(z)^2+\mathrm{Im}(z)^2}$$

2. $z$ 的幅角：称复平面上的有向线段$\overrightarrow{Oz}$与实轴正向的夹角$\theta$为$z$的辐角。

约定：
$\theta\geq0$：当实轴的正方向向量按逆时针旋转角度$\theta$到有向线段$\overrightarrow{Oz}$ 时。
$\theta<0$：当顺时针旋转角度$\theta$到有向线段$\overrightarrow{Oz}$时。

3. $z$的三角函数形式：

$$z=|z|\cos\theta+|z|\sin\theta\mathrm{i}$$

二、共轭复数

已知复数$z=a+b\boldsymbol{i}$，这里$a,b\in\mathbb{R}$.我们称如下定义的复数：
$$\bar{z}=a+(-b)\mathrm{i}$$
为复数z的共轭复数。

在复平面上，复数与共轭复数关于实轴对称。

存在运算规律：$|z|^2=z\bar{z}$

三、复数的运算规律

1. 对于任意复数$z_1, z_2\in \mathbb{C}$，都有：$\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}$,

2. 复数的乘法运算是指任意两个复数的求积过程。两个复数的积如下定义并记号：
   对于给定的两个复数
   这里$a_1, b_1, a_2, b_2\in \mathbb{R}$.
   $$z_1=a_1+b_1\mathrm{i},\quad z_2=a_2+b_2\mathrm{i}$$
   复数$z_1$与$z_2$的积是一个记为$z_1\cdot z_2$ 的新复数：
   $$z_1\cdot z_2=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)\mathrm{i}$$
   如同实数运算那样，我们也记$z^2=z\cdot z.$

   依据复数的乘法公式，可得如下重要等式：
   $$i^2=-1$$
   事实上，
   $$\mathrm{i}^2=(0+1\mathrm{i})(0+1\mathrm{i})=(0\cdot0-1\cdot1)+(0\cdot1+1\cdot0)\mathrm{i}=-1+0\mathrm{i}=-1.$$
   $\mathrm{i}^2=-1$ 往往被看成为之所以引入虚数单位的原因：为了解决$z^2+1=0$ 的求解问题
   我们也记：
   $$\mathrm{i}=\sqrt{-1}$$

3. 对于任意复数$z_1, z_2\in \mathbb{C}$，都有：$\overline{z_1z_2}=\overline{z_1}\, \overline{z_2}$,
4. 复数的消去律：对于任意复数$z_1, z_2\in \mathbb{C}$，若$z_1 z_2 = 0$，则$z_1=0$或者$z_2=0$.

例1 证明复数的消去律。

证明：对于任意复数$z_1,z_2\in\mathbb{C}$，若 $z_1z_2=0$,则：
$$\mid z_1\mid^2\mid z_2\mid^2=\left(\overline{z_1}z_1\right)\left(z_2\overline{z_2}\right)=\overline{z_1}(z_1z_2)\overline{z_2}=\overline{z_1}\cdot0\cdot\overline{z_2}=0$$由于$|z_1|^2,|z_2|^2$均为实数，依实数乘法运算的消去律，我们有$|z_1|^2=0$或$|z_2|^2=0$.
当$|z_1|^2=0$时，依复数模长的计算公式，我们有$\operatorname{Re}(z_1)=\operatorname{Im}(z_1)=0$，故 $z_1=0$.
同理可证，当$|z_2|^2=0$时，$z_2=0$.
综上所述，我们有$z_1=0$ 或$z_2=0$.

5. 若 $z_{1}= a_{1}+ b_{1}\mathrm{i}$，$z_{2}= a_{2}+ b_{2}\mathrm{i}$，这里 $a_{1}, b_{1}, a_{2}, b_{2}\in \mathbb{R}$，且 $a_{2}^{2}+ b_{2}^{2}\neq 0$，则不难知：
   $$z_1\div z_2=\frac{z_1\overline{z_2}}{z_2\overline{z_2}}=\frac{1}{|z_2|^2}z_1\overline{z_2}=\frac{a_1a_2+b_1b_2}{a_2^2+b_2^2}+\frac{a_2b_1-a_1b_2}{a_2^2+b_2^2}\mathrm{i}$$

6. 复数的三角不等式：对于任意复数 $z_1,z_2\in\mathbb{C}$，$| z_1+ z_2| \leq | z_1| + | z_2|$.

   四、复数乘除法的几何意义

对于任意复数$z_1,z_2\in\mathbb{C}$,不妨设：

$$z_1=|z_1|(\cos\theta_1+\sin\theta_1\mathrm{i}),z_2=|z_2|(\cos\theta_2+\sin\theta_2\mathrm{i})$$

这里 $\theta_1,\theta_2$分别是复数$z_1,z_2$ 的辐角。则依复数加法及乘法运算的规律，我们有：

$$\begin{aligned}z_{1}z_{2}&=\:|\:z_{1}\:|\:|\:z_{2}\:|\left[\left(\cos\theta_{1}\cos\theta_{2}-\sin\theta_{1}\sin\theta_{2}\right)+\left(\cos\theta_{1}\sin\theta_{2}+\sin\theta_{1}\cos\theta_{2}\right)\mathrm{i}\right]\\&=\:|\:z_{1}\:|\:|\:z_{2}\:|\left[\cos(\theta_{1}+\theta_{2})+\sin(\theta_{1}+\theta_{2})\mathrm{i}\right].\end{aligned}$$

也就是说，两个复数相乘，在复平面上就是两个复数的模长相乘，辐角相加。

同样地，复数除法的几何意义是在复平面内，商的模等于被除数和除数的模的商，商的辐角等于被除数和除数的辐角的差。

五、复数的欧拉（Euler）公式

复数的欧拉公式表达式为：

$$\mathrm{e}^{\mathrm{i}\theta}=\cos\theta+\sin\theta\mathrm{i}$$

若复数$z=|z|(\cos\theta+\sin\theta \mathrm{i})$，则：

$$z=|z| e^{i\theta}$$

在欧拉公式中，令 $\theta=\pi$并移项，则：

$$\mathrm{e}^{\mathrm{i}\pi}+1=0$$

六、复数的棣莫弗（De Moivre）公式

复数的棣莫弗公式表达式为：

$$(\cos\theta+\sin\theta\mathrm{i})^n=\cos n\theta+\sin n\theta\mathrm{i},n\geq1$$

例2 证明棣莫弗公式

证明：对$n\in\mathbb{Z}^*$，采用数学归纳法证明。
当$n=1$时，等式明显成立。
设当$n=k$时等式成立，则当$n=k+1$时：
$$\begin{aligned}\left[r\left(\cos\theta+\mathrm{i}\sin\theta\right)\right]^{k+1}&=r^{k+1}(\cos\theta+\mathrm{i}\sin\theta)^k\cdot\left(\cos\theta+\mathrm{i}\sin\theta\right)\\&=r^{k+1}\left(\cos k\theta+\mathrm{i}\sin k\theta\right)\left(\cos\theta+\mathrm{i}\sin\theta\right)\\&=r^{k+1}\left[\cos k\theta\cos\theta+\mathrm{i}\left(\sin k\theta\cos\theta+\cos k\theta\sin\theta\right)-\sin k\theta\sin\theta\right]\\&=r^{k+1}\left[\cos(k+1)\theta+\mathrm{i}\sin(k+1)\theta\right]\end{aligned}$$
即当$n=k+1$时等式也成立。
综上，对于任意正整数$n$，都有$\left[r\left(\cos\theta+\mathrm{i}\sin\theta\right)\right]^n=r^n\left(\cos n\theta+\mathrm{i}\sin n\theta\right)$

借助欧拉公式，我们可以非常容易地证明上述公式。

例3 用欧拉公式证明棣莫弗公式

证明：把所有的复数改写成指数的形式，即$z_1=r_1\mathrm{e}^{\mathrm{i}\theta_1},z_2=r_2\mathrm{e}^{\mathrm{i}\theta_2},\cdots,z_n=r_n\mathrm{e}^{\mathrm{i}\theta_n}$
则$z_1z_2\cdots z_n=r_1r_2\cdots r_n\mathrm{e}^{\mathrm{i}(\theta_1+\theta_2+\cdots+\theta_n)}$

使用欧拉公式展开可以得到棣莫弗公式。

若复数$z=|z|(\cos\theta+\sin\theta \mathrm{i})$，则：

$$z^n=|z|^n(\cos n\theta+\sin n\theta\mathrm{i}),n\geq1$$