实数基础知识

文章	评论	标签
117	20	28

引言

数学粗略地说是由三个大的分支组成：几何学、代数学和分析学。他们都离不开数这个基本概念。例如从“微积分”开始的分析学，是建立在严格的极限理论基础上的，而这一理论所依赖的就是实数体系的连续性。因此，要学好数学，必须先学习数的理论。

一、素数

1、素数的定义与检验

素数在数中占有异乎寻常的地位，素数的理论初步建立在欧几里得的《几何原本》之中。定义为一个大于 $1$ 的自然数，如果除了 $1$ 和其自身外，不能被其他自然数整除，则称此自然数为素数（质数），否则称为合数。例如： $2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47. . . . . .$ 都是素数。

【注】 $0$ 和 $1$ 既不是素数，也不是合数。

检验素数的基本方法：用 $2$ 到 $\sqrt{n}$ 之间的所有整数去除 $n$ ，均无法整除，则 $n$ 为素数。

2、素数的性质

定义：若只有 1 能同时整除自然数 $M$ 与 $N$ ，即不存在大于 $1$ 的自然数同时整除 $M$ 与 $N$ , 则称 $M$ 与 $N$ 为互素的（或互质的）。

定理 1： 互素的两个自然数是与它们有同比自然数对中最小的。即：设 $m, n, p, q$ 为自然数，如果 $\frac{p}{a} = \frac{m}{n}$ ,且 $p, q$ 互素，则 $p \leq m, q \leq n$ .

定理 2：（欧几里得引理）若素数 $p$ 整除两自然数之积 $a b$ (记为 $p ∣ a b$ ), 则 $p ∣ a$ （ $p$ 整除 $a$ ）或 $p ∣ b$ （ $p$ 整除 $b$ ）.

定理 3：（裴蜀定理）若 $a, b$ 是整数，且它们的最大公约数 $gcd (a, b) = d$ ，那么对于任意的整数 $x$ 和 $y$ ，整数 $a x + b y$ 必是 $d$ 的倍数。特别地，一定存在整数 $x, y$ ，使 $a x + b y = d$ 成立。
推论： $a, b$ 互素的充分必要条件是存在整数 $x, y$ 使 $a x + b y = 1$

例 1：求平面上整点 (两个坐标皆为整数的点) 到直线 $y = \frac{5}{3} x + \frac{4}{5}$ 的距离的最小值。
解：由点到直线的距离公式知整点 $(m, n)$ 到 $y = \frac{5}{3} x + \frac{4}{5}$ 的距离为，而 $gcd (25, 15) = 5$ 由裴蜀定理知 $25 m - 15 n$ 为 $5$ 的倍数，所以当 $25 m - 15 n = - 10$ 时， $d$ 取最小值：
$d_{min} = \frac{2}{5 \sqrt{34}} = \frac{\sqrt{34}}{85}$

定理 4：（算术基本定理）任何一个大于 $1$ 的自然数 $N$ ，如果不是素数，那么 $N$ 可以唯一分解为有限个素数的乘积： $N = p_{1}^{a_{1}} p_{2}^{a_{2}} \dots p_{n}^{a_{n}}$ ，其中 $0 < p_{1} < p_{2} < \dots < p_{n}$ 为素数，指数 $a_{i} (i = 1, 2, \dots, n)$ 为正整数。例如 $12 = 2^{2} \times 3$ ， $60 = 2^{2} \times 3 \times 5$ ， $15246 = 2 \times 3^{2} \times 7 \times 11^{2}$ 等等。

定理 5：素数有无穷多个。

证明：用反证法。假设素数只有有限多个，设为 $k$ 个： $p_{1}, p_{2}, \dots, p_{k}$ .
记 $N = p_{1} p_{2} \dots p_{k}$ ，有 $N + 1 > p_{i} (i = 1, 2, \dots, k)$ .
那么：
若 $N + 1$ 为素数，则与“素数只有 $k$ 个”矛盾；
若 $N + 1$ 为合数 , 则 $N + 1$ 可分解为若干个比它小的素数之积，而 $N + 1$ 不可能被 $p_{i} (i = 1, 2, \dots, k)$ 整除，所以还存在不同于 $p_{i} (i = 1, 2, \dots, k)$ 的素数，这又与“素数只有 $k$ 个”这个假设矛盾。
综上可得，素数有无穷多个。

3、孪生素数和哥德巴赫猜想

相差 $2$ 的两个素数称为孪生素数。例如： $3$ 和 $5$ ， $11$ 和 $13$ ， $17$ 和 $19$ ， $41$ 和 $43$ 等等。“存在无穷多对孪生素数”这就是著名的孪生素数猜想，至今未得到证明，但数学家们相信这是正确的。

数论是数学的一个重要分支，主要研究整数性质以及和它有关的规律与理论。数论研究中最著名的猜想应该是“哥德巴赫猜想 " 了。1742 年，哥德巴赫给欧拉的信中提出了：“任一大于 $2$ 的偶数都可表示成两个素数之和。"这就是著名的哥德巴赫猜想，我们常常简称为“1+1”。

三、有理数和无理数

1、有理数的性质

有理数四则运算的封闭性：有理数与有理数进行加减乘除运算后还是有理数。
有理数的稠密性：任意两个不同的有理数之间存在无数个有理数。
有理数的可公度性：所谓可公度量，亦称为可通约量，是数学的基本概念之一，指两个同是第三个量的整数倍的量.对于两个量 $A$ 与 $B$ ,若存在第三个量 $C$ , 使 $A = p C, B = q C$ 同时成立，这里 $p, q$ 为自然数，则称量 $A$ 与量 $B$ 可公度或可通约，且称 $C$ 是 A 与 $B$ 的一个公度，这时称 $A$ 与 $B$ 是可公度量或可通约量.若不存在自然数 $p, q$ 与量 $C$ ,使 $A = p C, B = q C$ 成立，则称 $A$ 与 $B$ 是不可公度或不可通约，这时 $A, B$ 是不可公度量或不可通约量。
任意两个有理数 $r_{1}$ 和 $r_{2}$ 存在公倍数，即 $\exists m, n \in Z, m r_{1} = n r_{2}$ ，设 $r_{1} = \frac{m_{1}}{n 1}, r_{2} = \frac{m 2}{n 2}$ ，那么有 $(m_{2} n_{1}) r_{1} = m_{1} m_{2} = (m_{1} n_{2}) r_{2}$
（可公度性的集合意义）辗转相截：两条线段 $a, b$ 长度为有理数，用 $b$ 去截 $a$ ，若剩下 $c (0 < c < b)$ ，则用 $c$ 去截 $b$ ，若剩下 $d (0 < d < c)$ 。则用 $d$ 去截 $c \dots$ 必可经有限次相截刚好截完。
设 $a = \frac{m_{1}}{n_{1}}, b = \frac{m_{2}}{n_{2}}$ ,则
$a = m_{1} n_{2} (\frac{1}{n_{1} n_{2}}) = m_{1} n_{2} r b = m_{2} n_{1} (\frac{1}{n_{1} n_{2}}) = m_{2} n_{1} r$
其中 $r = \frac{1}{n_{1} n_{2}}$ 为 $a, b$ 的一个公度。

2、无理数的性质

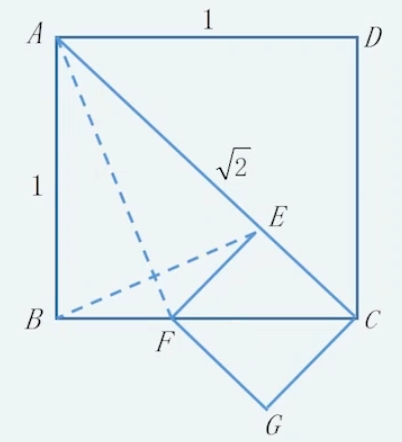
正方形的边长与其对角线长不可公度：
如图，设正方形边长为 $1$ ，将边长与对角线辗转相截：在 $A C$ 上截得 $A E = A B$ ，过点 $A$ 作 $B F$ 的垂直平分线。有 $∠ A B F ≅ ∠ A E F$ ，于是 $B F = E F$ ，接下来即为小正方形 $C E F G$ 的边长 $E F$ 去截其对角线 $F C$ ，这样可以无穷无尽地截下去，永远截不完 ......
定义：不能表示成两个整数之比的数称为无理数。
例 2： $\sqrt{2}$ 是无理数
证明：（反证法）假设 $\sqrt{2} = \frac{m}{n}$ （ $m, n$ 为互素的正整数），那么有 $2 n^{2} = m^{2}$ ，所以 $m$ 是偶数，记 $m = 2 k, k \in Z^{+} \Rightarrow n^{2} = 2 k^{2} \Rightarrow n$ 是偶数，与 $m, n$ 互素矛盾。因此 $\sqrt{2}$ 是无理数。
例 3：证明：如果 $n$ 不是完全平方数（等于某整数的平方的正整数），则 $\sqrt{n}$ 为无理数。
证明：（反证法）假设 $\sqrt{n} = \frac{p}{q} (p, q 为互素的正整数)$ ，那么 $n q^{2} = p^{2}$ .
因为 $n$ 不是完全平方数，所以 $\sqrt{n} = \frac{p}{q}$ 不是整数，存在 $k \in Z^{+}$ 使得 $k < \frac{p}{q} < k + 1$ ，即 $0 < p - k q . < q$ .
考察 $p (p - k q) = p^{2} - k p q = n q^{2} - k p q = q (n q - k p)$ ，于是有 $\frac{p}{q} = \frac{n q - k p}{p - k q} = \frac{p_{1}}{q_{1}}$ .其中 $q_{1} = p - k q < q \Rightarrow p_{1} < p$ .也就是说可找到正整数 $p_{1} < p, q_{1} < q$ ,使得假设 $\frac{p_{1}}{q_{1}} = \frac{p}{q};$ 那么用 $p_{1}, q_{1}$ 代替 $p, q$ 可进行以上“操作”，又可以找到正整数 $p_{2} < p_{1}, q_{2} < q_{1}$ ，使得假设 $\frac{p_{1}}{q_{1}} = \frac{p_{2}}{q_{2}} \cdot \dots \dots$
这样的“操作”可以一直进行下去，这是不可能的，因为 $p, q$ 是有限的自然数。矛盾。
从以上例子可以看到，无理数有无穷多个。

其实，无理数远不止这些 $\sqrt{n}$ .有理数与无理数统称为实数，实数布满了整个数轴。

四、代数数与超越数（实数范围内）

代数数定义：如果 $b$ 是某整系数多项式 $a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{1} x + a_{0}$ （其中 $n$ 为正整数， $a_{n} \neq 0$ , $a_{k}$ 为整数， $k = 1, 2, 3, \dots, n$ ）的根，则称 $b$ 为代数数。

例如：
(1) 任意有理数 $\frac{m}{n}$ 为代数数，因为它是一次整系数多项式 $n x - m$ 的根。
(2) $\sqrt{2}$ 是代数数，因为它是二次整系数多项式 $x^{2} - 2$ 的根。

代数数经加、减、乘、除（分母不为零）四则运算后仍为代数数。
不是代数数的数称为超越数，例如 $π, e$ 是超越数。
可以证明，当 $a \neq 0$ 为有理数时， $\sin a π, \cos a π$ 是代数数，而 $\sin a, \cos a$ 是超越数。

五、等势集与可列集

定义：设 $A, B$ 为两个集合，如果存在一个从 $A$ 到 $B$ 的一一对应映射 (双射)，则称集合 $A$ 与集合 $B$ 等势，也称 $A$ 与 $B$ 是等势集。记作 $A \sim B$ .
两个有限集合等势当且仅当两个集合的元素个数相等。
空集只与空集自身等势。
等势具有如下性质：
(1) 自反性： $A \sim A$ .
(2) 对称性：若 $A \sim B$ ,则 $B \sim A$ .
(3) 传递性：若 $A \sim B, B \sim C$ ,则 $A \sim C$ .

例如：
全体正整数集 $N^{+} = {1, 2, 3, . . .}$ 和全体偶数集 ${2, 4, 6, . . .}$ 等势。可作双射 $f (n) = 2 n, n = 1, 2, 3, \dots$
自然数集和全体整数集等势。可作双射 $f (n) = {\begin{cases} k, & n = 2 k \\ - (k + 1), & n = 2 k + 1 \end{cases}, k = 0, 1, 2, 3, \dots$

定义：如果集合 $A$ 与自然数集等势，则称集合 $A$ 是可列的（或可数的）。对应之前所学：可数集。
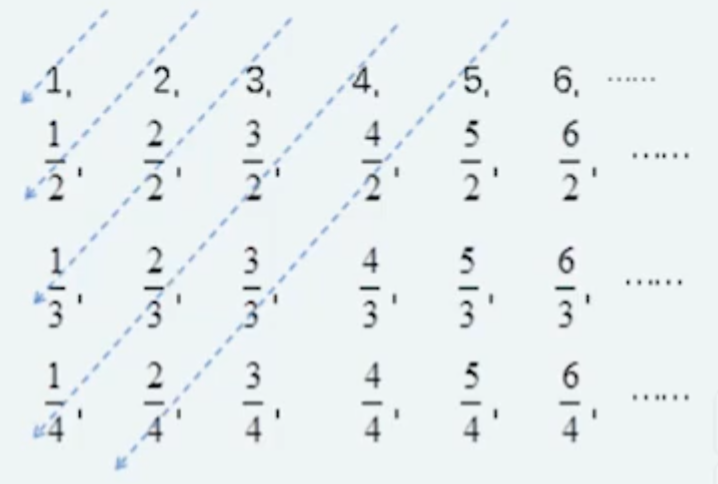
正整数集、整数集都是可列的，全体有理数集也是可列的。我们只要考虑全体有理数集中的元素是否可以排成一个队列，显然只要考虑正有理数的情形即可。我们以有理数（分数）的分母大小为序，写出所有正有理数如下：
现从左上角开始，按箭头方向将所有的数排成队列 (跳过前面已出现的数字
$1, 2, \frac{1}{2}, 3, \frac{1}{3}, 4, \frac{3}{2}, \frac{2}{3}, \frac{1}{4}, 5, \frac{1}{5}, 6, \dots$ ，
这样就把所有的正有理数排成队列了。如果我们将 $0$ 排在第一位，然后将每个正有理数的相反数插入到自己的后面，那么就把全体有理数排成队列了，因此全体有理数集是可列的。
$[a, b]$ 上的实数与 $[c, d]$ 上的实数是等势的。 $(0, 1)$ 上的实数与实数集 $R$ 也是等式的。
反证法证明全体实数是不可列的（无理数是不可列的），即证 $(0, 1)$ 上的实数是不可列的。
假设 $(0, 1)$ 上的实数可列。
我们用小数表示，可和自然数对应如下：
$0 \leftrightarrow 0. \overset{―}{a_{1} a_{2} a_{3} a_{4} a_{5} \dots}$
$1 \leftrightarrow 0. \overset{―}{b_{1} b_{2} b_{3} b_{4} b_{5} \dots}$
$2 \leftrightarrow 0. \overset{―}{c_{1} c_{2} c_{3} c_{4} c_{5} \dots}$
$3 \leftrightarrow 0. \overset{―}{d_{1} d_{2} d_{3} d_{4} d_{5} \dots}$
$⋮$
现取 $(0, 1)$ 内一数 $a = 0. \overset{―}{p_{1} p_{2} p_{3} p_{4} p_{5} \dots}$ ，使得： $p_{1} \neq a_{1}, p_{2} \neq b_{2}, p_{3} \neq c_{3}, p_{4} \neq d_{4}, \dots$ （且 $p_{k} \neq 0, 9$ ）这样，数 $a$ 不在对应的队列中，因为 $a$ 和队列中的数至少有一位数字不同。矛盾。
所以， $(0, 1)$ 上的实数不可列。即全体实数（无理数）是不可列的。
若集合 $A, B$ 可列，那么集合 $A \cup B$ 是可列的。
现取无理数集的一个真子集：
$W = {\sqrt{2}, 2 \sqrt{2}, 3 \sqrt{2}, 4 \sqrt{2}, 5 \sqrt{2}, \dots}$ ,显然它与有理数可一一对应，即与有理数集等势，所以说无理数此有理数多。
另外可以证明：全体代数数集是可列的，全体超越数集是不可列的。