一、奥托循环(Otto Cycle)
1. 循环过程描述
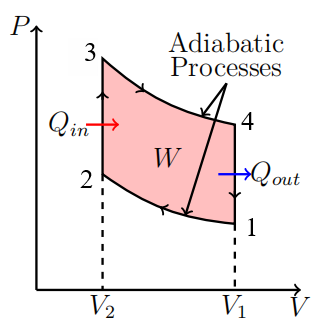
奥托循环由四个过程组成(以理想气体为工质):
- $1 \rightarrow 2$:绝热压缩
- $2 \rightarrow 3$:等容加热(燃烧过程,吸热$Q_\mathrm{in}$)
- $3 \rightarrow 4$:绝热膨胀
- $4 \rightarrow 1$:等容冷却(排气,放热$Q_\mathrm{out}$)
2、过程物理量变化与公式推导
(1)绝热过程($1\rightarrow2$, $3\rightarrow4$)
绝热条件下,
$$ pV^\gamma = \mathrm{const} $$
$$ TV^{\gamma-1} = \mathrm{const} $$
其中$\gamma = C_p/C_v$。
设$V_1$为初始体积,$V_2$为压缩后体积,压缩比$r = V_1 / V_2$,则
$$ \frac{T_2}{T_1} = \left(\frac{V_1}{V_2}\right)^{\gamma-1} = r^{\gamma-1} $$
同理,
$$ \frac{T_3}{T_4} = r^{\gamma-1} $$
(2)等容过程($2\rightarrow3$, $4\rightarrow1$)
等容加热:
$$ Q_\mathrm{in} = mC_v (T_3 - T_2) $$
等容放热:
$$ Q_\mathrm{out} = mC_v (T_4 - T_1) $$
3、效率推导
热效率定义为
$$ \eta_\mathrm{Otto} = 1 - \frac{Q_\mathrm{out}}{Q_\mathrm{in}} $$
代入上式得到
$$ \eta_\mathrm{Otto} = 1 - \frac{T_4 - T_1}{T_3 - T_2} $$
利用绝热关系:
$$ T_2 = T_1 r^{\gamma-1} $$
$$ T_4 = T_3 / r^{\gamma-1} $$
代入得
$$ \eta_\mathrm{Otto} = 1 - \frac{T_3 / r^{\gamma-1} - T_1}{T_3 - T_1 r^{\gamma-1}} $$
若燃烧后温度远大于初温($T_3 \gg T_1$),可近似为
$$ \eta_\mathrm{Otto} \approx 1 - \frac{1}{r^{\gamma-1}} $$
4、物理量变化计算方法
- 温度:绝热过程由压缩比决定,等容过程突变。
- 压力:可用理想气体状态方程$pV = nRT$结合温度和体积变化计算。
- 体积:等容过程不变,绝热过程按压缩比变化。
- 做功/吸放热:等容过程吸放热,绝热过程为做功。
二、卡诺循环(Carnot Cycle)
1、循环过程描述
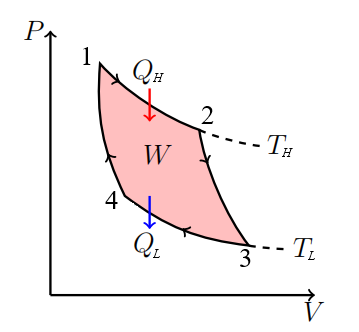
卡诺循环包含:
- $1 \rightarrow 2$:等温膨胀(高温热源,温度$T_H$,吸热$Q_H$)
- $2 \rightarrow 3$:绝热膨胀(温度降至$T_L$)
- $3 \rightarrow 4$:等温压缩(低温热源,温度$T_L$,放热$Q_L$)
- $4 \rightarrow 1$:绝热压缩(温度升至$T_H$)
2、过程物理量变化与公式推导
(1)等温过程($1\rightarrow2$, $3\rightarrow4$)
等温膨胀吸热:
$$ Q_H = nRT_H \ln\left(\frac{V_2}{V_1}\right) $$
等温压缩放热:
$$ Q_L = nRT_L \ln\left(\frac{V_4}{V_3}\right) $$
(2)绝热过程($2\rightarrow3$, $4\rightarrow1$)
绝热过程满足
$$ T_H V_2^{\gamma-1} = T_L V_3^{\gamma-1} $$
$$ T_L V_4^{\gamma-1} = T_H V_1^{\gamma-1} $$
3、效率推导
循环净做功:
$$ W_\mathrm{net} = Q_H - |Q_L| $$
热效率定义为
$$ \eta_\mathrm{Carnot} = 1 - \frac{|Q_L|}{Q_H} $$
由体积与温度关系可得
$$ \frac{V_2}{V_1} = \frac{V_3}{V_4} $$
所以
$$ \ln\left(\frac{V_2}{V_1}\right) = \ln\left(\frac{V_3}{V_4}\right) $$
则
$$ \eta_\mathrm{Carnot} = 1 - \frac{T_L}{T_H} $$
4、物理量变化计算方法
- 温度:等温过程恒定,绝热过程变化。
- 压力、体积:理想气体状态方程结合过程类型推算。
- 做功/吸放热:等温过程有热量交换,绝热过程无热量交换。
三、两种循环的比较
| 项目 | 奥托循环 | 卡诺循环 |
|---|---|---|
| 热效率 | $1 - \frac{1}{r^{\gamma-1}}$ | $1 - \frac{T_L}{T_H}$ |
| 吸/放热过程 | 等容过程 | 等温过程 |
| 理论极限 | 否 | 是 |
| 实际应用 | 内燃机理想模型 | 理论模型,不可实现 |
| 关键参数 | 压缩比、比热比 | 热源温度 |



对了,博客之前的友链,现已更名。
原名:春花秋月
新名:我的飛鳥集
麻烦有空更改呢~
地址:https://www.explorexd.com
图标:https://halo.cos.explorexd.com/halo/jack.jpeg
描述:莫愁前路无知己,天下谁人不识君。
RSS:https://www.explorexd.com/rss.xml
已添加贵站